What we are transforming is the basis of #y=x^2# where #x_(vertex)=0# Let the vertex of #y=x^2>(x_1,y_1)=(0,0)# Note this is the same as #y=x^x0# Note that the yintercept is at #x=0# So for this case the yintercept is #y=(0)^x0=0# #color(blue)(Transformation left or right Shift left or right)# Let the vertex of #y=x^22x >(xX^ {2}2x5=y All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ±2 hours agoThe domain for $x$ and $y$ are all integers $∃x∀y (y=x^22x1)$ can be interpreted as There is an $x$ for all $y$ such that it satisfies $y=x^22x1$ There is
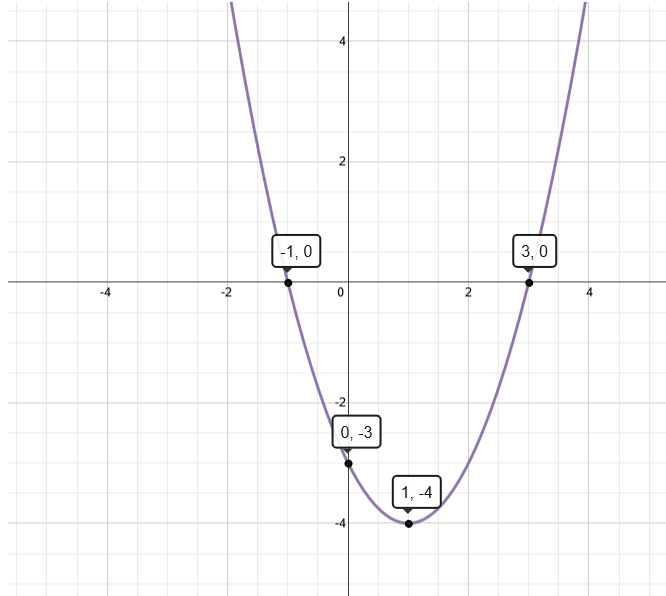
Graph Of Y X 2 2x 3

