Kenar uzunlukları 15 75 90 üçgeni 643124-15 75 90 üçgeni kenar uzunlukları

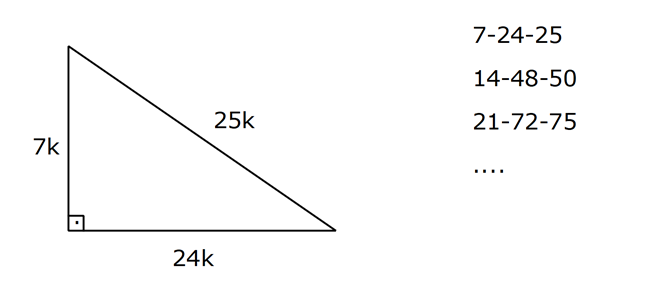
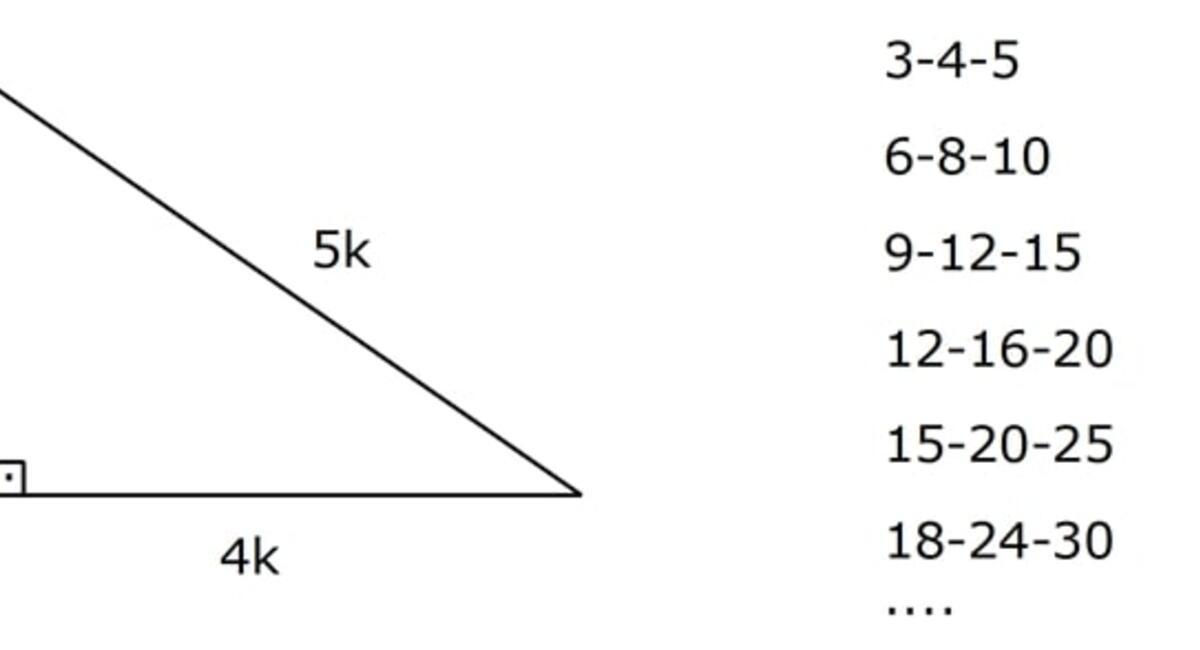
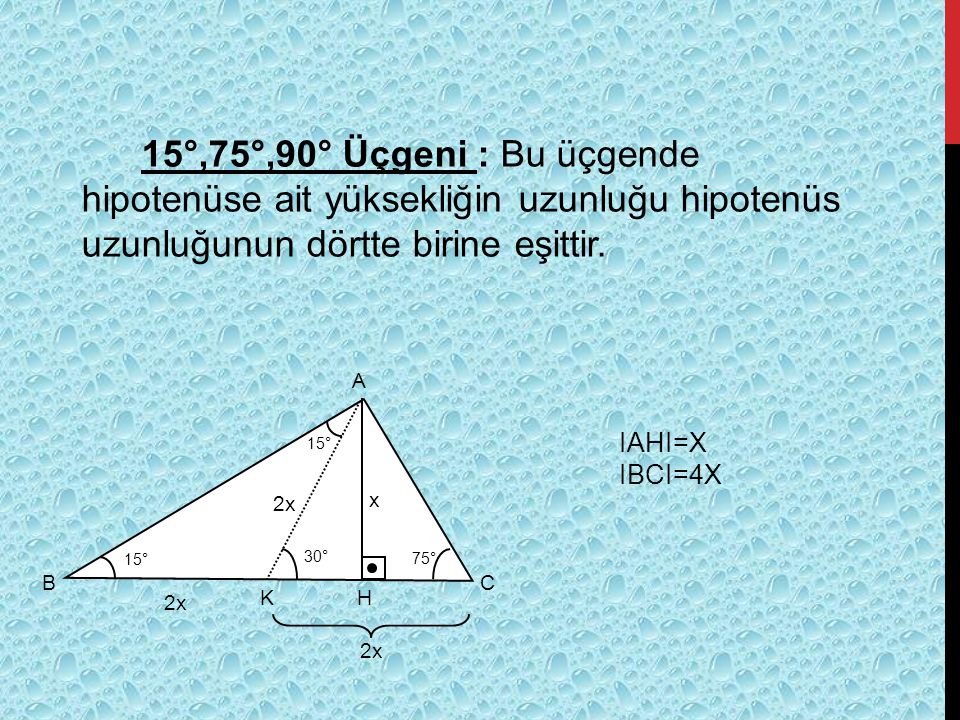
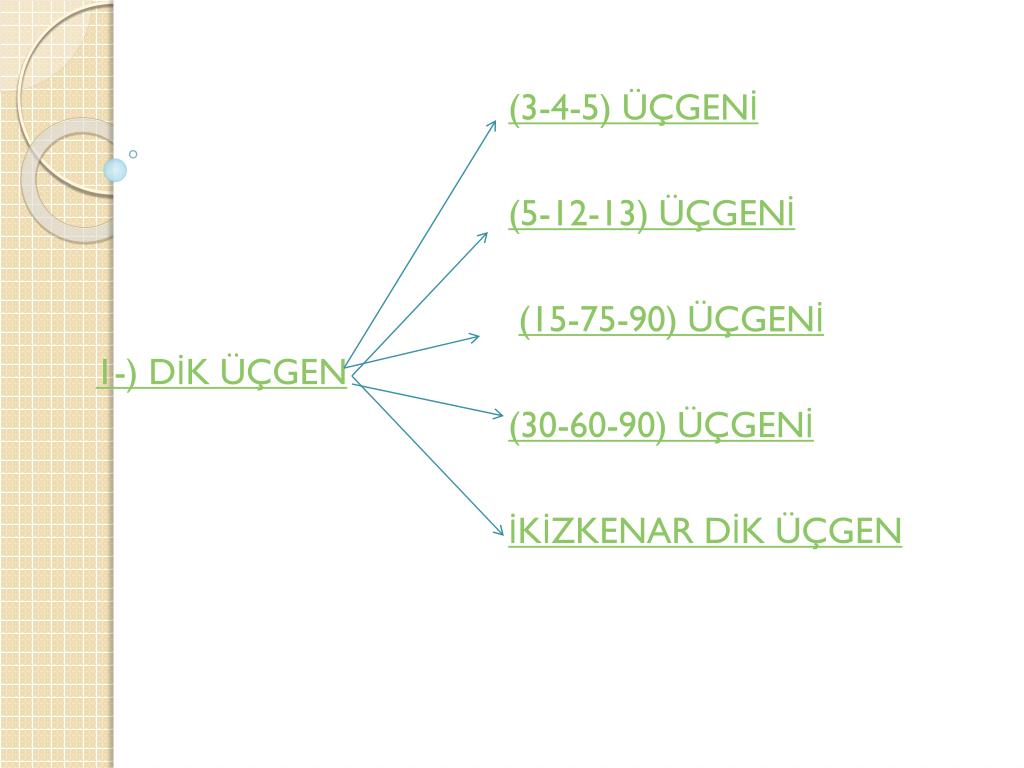
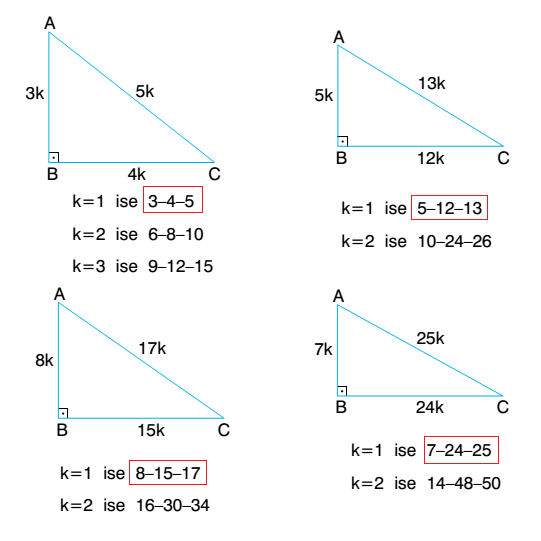
15 75 90 Üçgeni alan ve kenar bağıntıları konu anlatımı 22 Kasım 21 aynagazete 0 yorum Özel üçgenler geometri de soru çözümü esnasında faydalanılan kurallar arasında yer almaktadır 15 75 90 üçgeni bir dik üçgen olarak bilinmektedir Tüm üçgenlerde olduğu gibi 15 75 90 üçgeninde Dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittirABC üçgeninde m (A) = 90° a 2 =b 2 c 2 ÖZEL DİK ÜÇGENLER 1 (3 – 4 – 5) Üçgeni Kenar uzunlukları (3 – 4 – 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir (6 – 8 – 10), (9 – 12 – 15), gibi 2 (5 – 12 – 13) Üçgeni15 75 90 üçgeni kenarları belirli orana sahiptir Bu oranların ezbere bilinmemesi halinde kendiliğinden bulmak da mümkün olabilmektedir Fakat bu oranları bilmek soruların çözülmesi için daha büyük kolaylık sunacaktır Buna göre 15 75 90 üçgeninde 15 karşısı 1 birim kabul edilirse 75'in karşısı kök 3 2 birim olmaktadır

Maxresdefault Jpg

15 75 90 üçgeni kenar uzunlukları

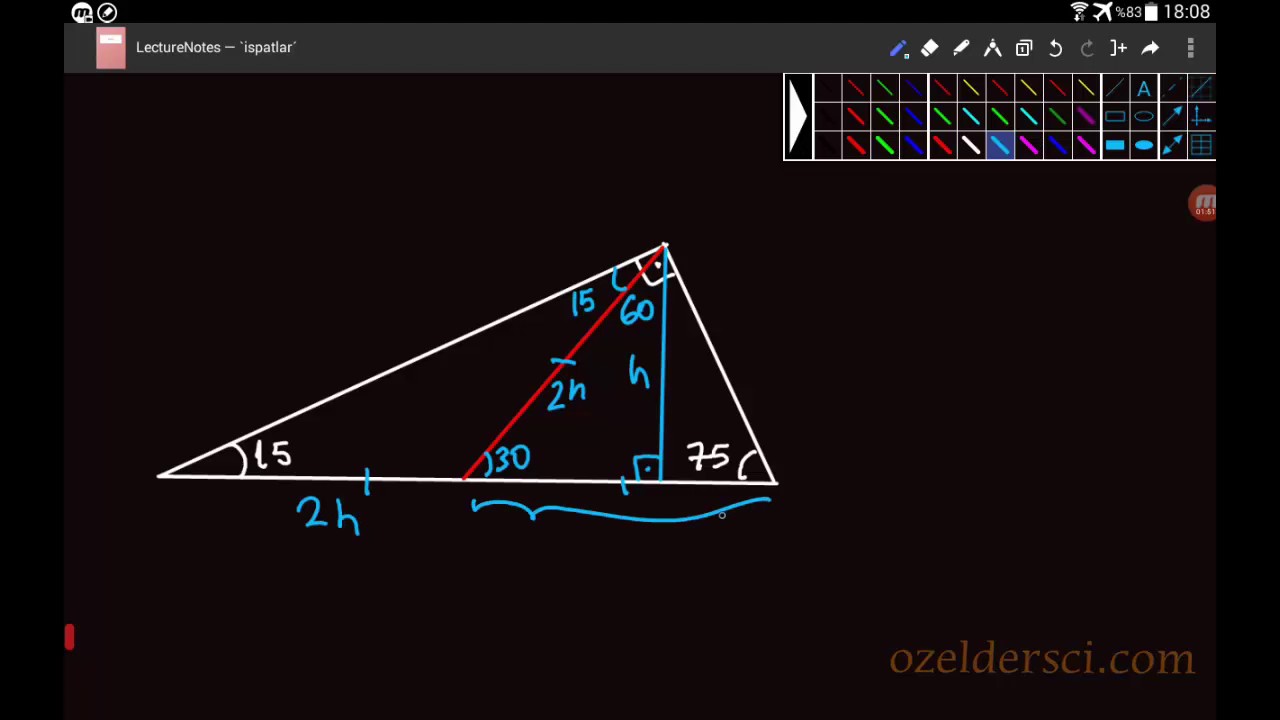
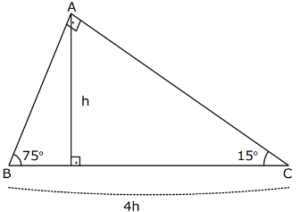
15 75 90 üçgeni kenar uzunlukları-90 derecenin karşısındaki kenar uzunluğu ise 60 derece ve 30 derecenin karşısındaki kenar uzunluklarının toplamına eşittir Örnek Bir (ABC) üçgeni varsayalım 'A' açısı = 30 'B' açısı = 60 'C' açısı = 90 Diyelim ve sadece 'A' karşı kenar uzunluğunu verelim ve BC = 2 cm ise bu göre;15 75 90 üçgeninde 90 derecelik açının gördüğü kenarın uzunluğuna bakılır Uzunluk ''4h'' olduğu takdir de ise bu kenarın yüksekliğinin ''h'' olması gerektiğini söylemek mümkündür

Ozel Ucgenler Konu Anlatimi

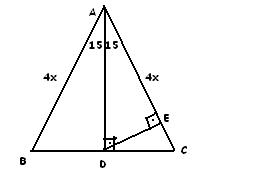
 2 (5 12 13) Üçgeni Kenar uzunlukları (5 12 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir (10 24 26), (15 36 39), gibi Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir Kenar uzunlukları 7,Kenarortay, hem yükseklik hem de açıortaydır Açıortay, hem yükseklik hem de kenarortaydır Yükseklik, hem kenarortay hem de açıortaydır Yani biri varsa, diğerleri de vardır  Üçgeni Kenar Bağıntısı ( İSPAT ) ADC Üçgeninin alanı da bunun yarısı 2x²'dir Aynı zamanda ADC üçgeninin Alanı = 1/24xDE 'dir 2x² = 2xDE DE=x bulunur ve üçgeninde AC uzunlugu DE uzunlugunun her zaman 4 Katıdır 02 Ağu 13 1958 #2

 15 75 90 Üçgeni;Hipotenüs, kendisine ait ola yüksekliğin 4Dik üçgenin açılarıyla kenar uzunlukları arasında herhangi bir oran yok kullanacağın formülşer var sadece a² b² = c² gibi Hipotenüs Uzunluğu 108,1666 birim Komşu Kenar Uzunluğu 90

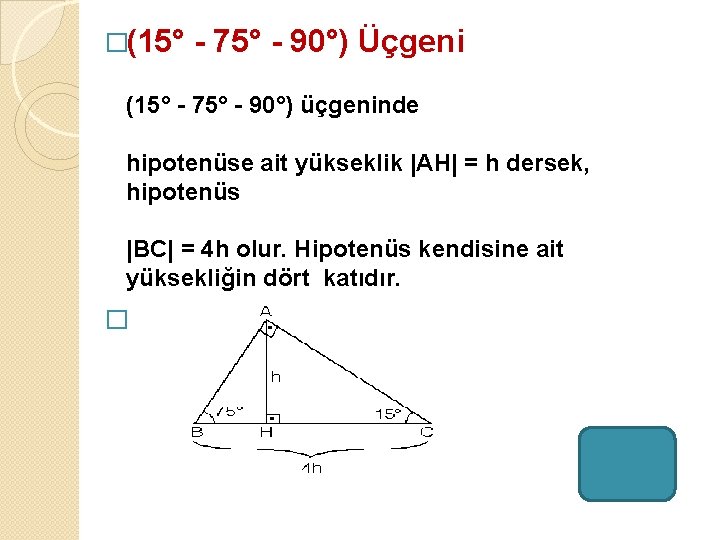
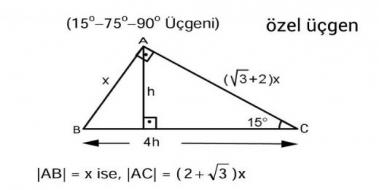
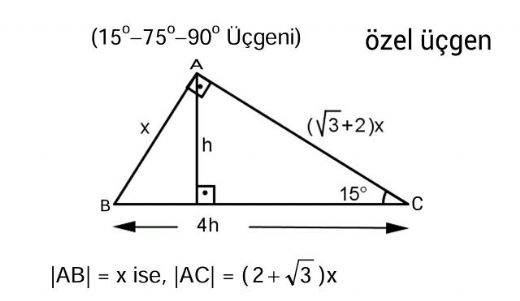
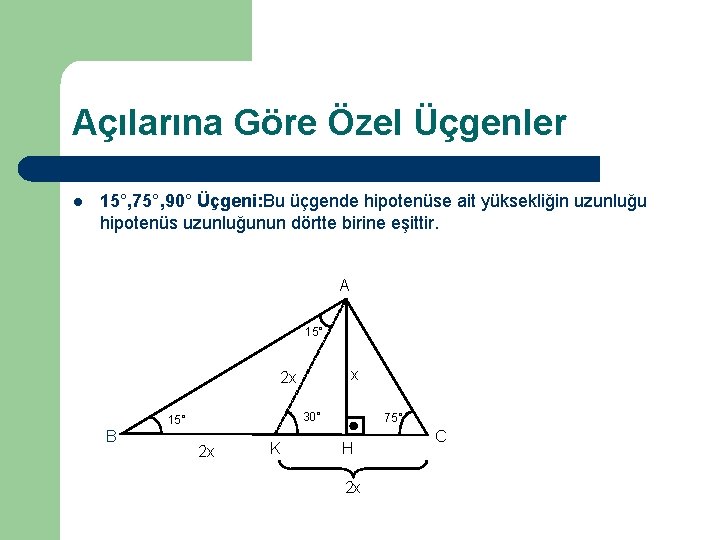
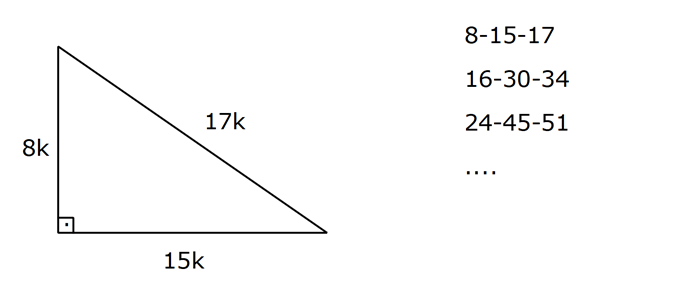
üçgeni değiştir kaynağı değiştir Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün katıdır Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdırKenar uzunlukları (8 15 17) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir (16 30 34), (24 45 51), gibi Uygulamamızdaki Sayıları Değiştirerek Sonuçları Gözlemleyiniz;

15 75 90 Triangle Proof Of Properties Youtube

Murat En Akdenz Nverstes Ge Nler 1

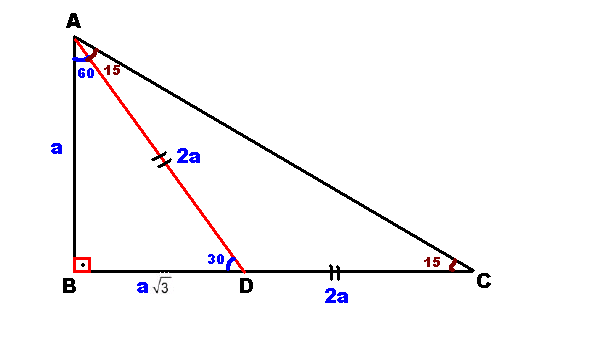
 Çözüm Verilen bilgi doğrultusunda üçgenin özel bir üçgen olduğu görülmektedir Bunun yanında 45 derecelik açının karşısındaki kenarın uzunluğu da 4 olarak verilmiş Buradan hareketle kuralın uygulaması yapılabilir Kural 90 derecelik açının karşısındaki kenarın uzunluğunun 4 sayısının kök 2 katı olduğunu söylemektedir(30° – 60° – 90°) dik üçgeninde; 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 in karşısındaki kenar "2aakök3"

Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik

Dik Acili Ucgen Kenarlarina Gore Ucgenler

Hipotenüs = 4 cm BC = 4 cm 5 (30° – 30° – 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH =(8 15 17) Üçgeni ;

Ozel Ucgenler Nelerdir Ozel Ucgen Ornekleri Ve Ozellikleri Egitim Haberleri

Ozel Ucgenler

 30 30 1 üçgende iki kısa kenar uzunlukları bir birlerine eşittir Uzun kenar bölümü kısa olan kenarın √3 katı olarak hesaplanır Eğer yöntemi aklınıza gelmeyecek olursa da kosinüs teorisini kullanarak aynı sonuca kendiniz de ulaşabilirsiniz 15 75 90 Üçgeni Özellikleri ve KuralıBir üçgende iç açıları toplamı 180 derece olduğu için diğer açı 1 = 15 işleminden 15 derece olarak bulunur Yani bu üçgen 15 75 90 üçgenidir Hipotenüsün uzunluğu bu kenara ait yüksekliğin 4 katı olduğu için 43 Bu dik üçgende kenar uzunlukları için Pisagor teoremi uygulanmaktadır 15 75 90 üçgeninin en önemli özelliği ise 90 derecelik açıdan indirilen yüksekliğin hipotenüs yani 90 derecelik açının gördüğü kenar uzunluğunun 1/4 'ü kadar olmasıdır Yani hipotenüs yüksekliğin 4 katı uzunluğundadır 15 75 90 ÜÇGENİ KURALI NEDİR?

Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Matematik

Beyza Nin Elinde Acilan 15 75 90 Olan Ucgen Gek Geometri

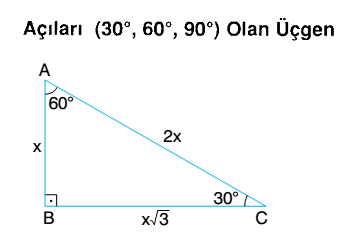
  üçgeni Kenar uzunlukları sayıları ve bu sayılarla orantılı olan bütün üçgenler dik üçgen kategorisine girer üçgeni Bu üçgende hipotenüsün sahip olduğu yükseklik h olarak kabul edilecek olursa, hipotenüs uzunluğu 4h olur Bir diğer deyişle;30°'nin karşısındaki kenar hipotenüsün yarısına eşittir 60° nin karşısındaki kenar, 30° nin karşısındaki 3 kenarın katıdır (30° – 30° – 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik15 75 90 üçgeni kenar uzunlukları 22 admin No Comments 15 75 90 üçgeni nasıl hesaplanır?

Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir

Th Q 15 17 Ucgeni

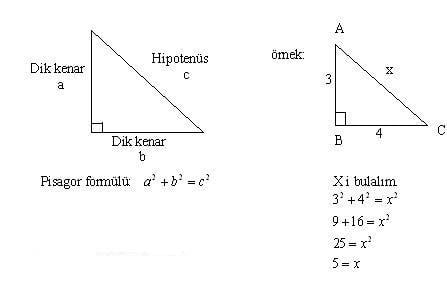
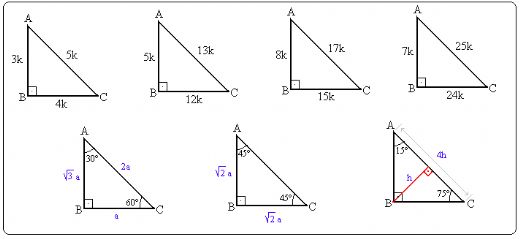
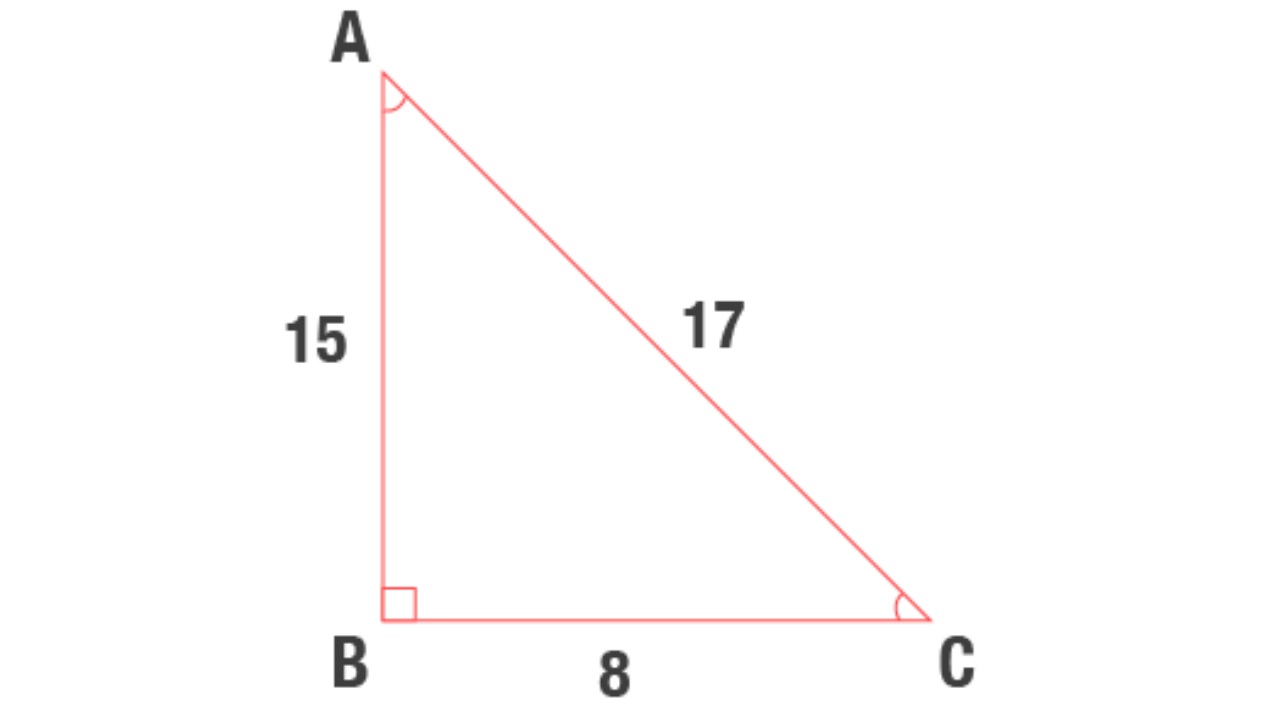
 Dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir ABC üçgeninde m (A) = 90° a2=b2c2 ÖZEL DİK ÜÇGENLER 1 (3 4 5) Üçgeni Kenar uzunlukları (3 4 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir (6 8 10), (9 12 15), gibi8 – 15 – 17 Üçgeni Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir 7 – 24 – 25 Üçgeni Kenar 15 – 75 – 90 Üçgeni 15° – 75° – 90° üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır Bunlar üçgeni üçgeni ve üçgenleridir Bu üçgenlerde Pisagor bağlantısı yardımı ile kenar uzunlukları bulunabilir Kenar uzunlukları bulunan dik üçgenin alanını hesaplamak ise mümkündür Dik üçgen alanını bulmak için basit bir formül bulunmaktadır Formül dik açılı üçgenin alanını

22 5 67 5 90 Ucgeni Ozelligi Matematik Sarisin Renkli Okuma

90 75 15 Ucgeni

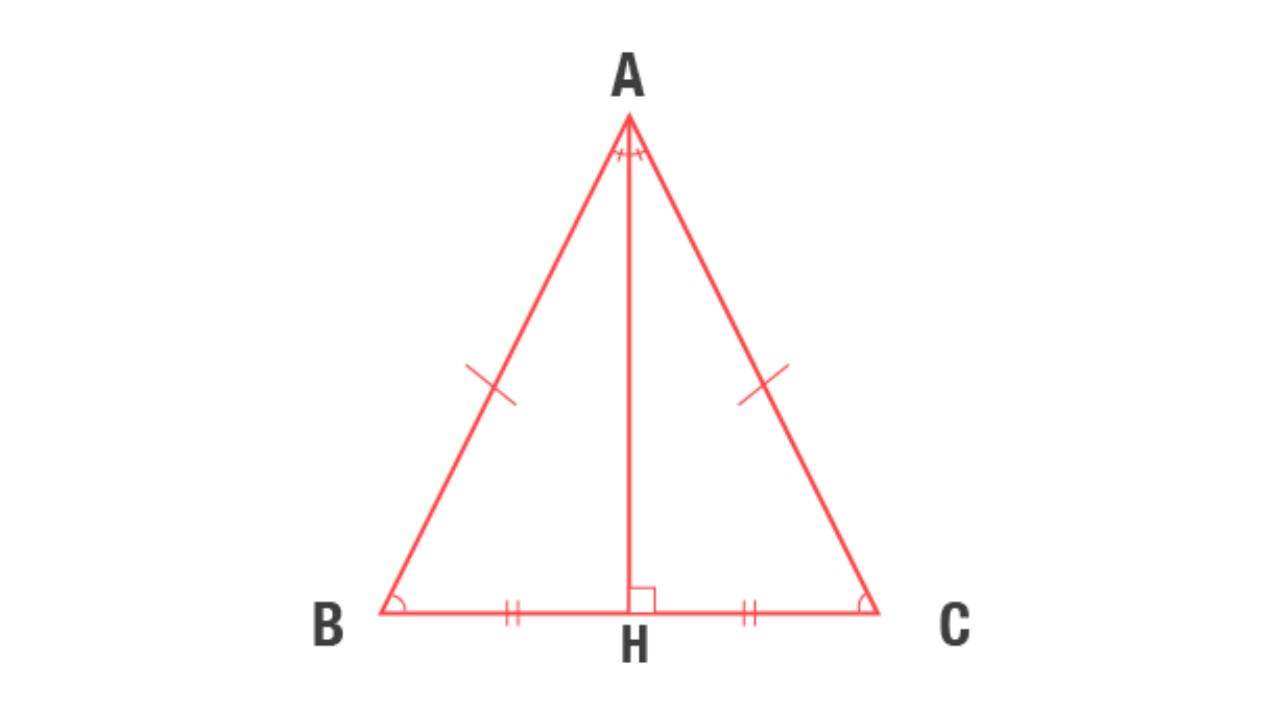
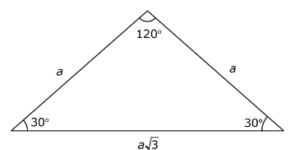
Özel üçgenler içinde yer alan eşkenar üçgen tüm kenar uzunlukları eşit olan üçgendir Eşkenar üçgende bütün yükseklik, kenarortay ve açıortay uzunlukları eşittir nA = nB = nC = Va = Vb = Vc = ha = hb = hc Bir eşkenar üçgenin iç bölgesinde herhangi bir yerinden alınan bir noktadan, kenarlara inilen dikmelerin 0 Üçgeni Üçgeni İKİZKENAR ÜÇGEN İkizkenar üçgende tepe açısından inen; 75 15 90 Özel Üçgeni Bu özel üçgende 15 derecelik açının karşısında yer alan kenar uzunluğu 1cm alınırsa 75 derecelik açının karşısındaki kenarın uzunluğu 2 √3 cm olur NOT 75 15 90 dik özel üçgeninde eğer hipotenüse bir dik indirilirse;

Net Fikir Ekim

15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Alan Ve Kenar Bagintilari Konu Anlatimi

 Uzun kenar (1 derece) x kök 3 cm;2 (5 12 13) Üçgeni Kenar uzunlukları (5 12 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir (10 24 26), (15 36 39), gibi Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dikÇokgenler Konu Anlatımı İçindekiler 15 75 90 Üçgeni Özellikleri

Murat En Akdenz Nverstes Ge Nler 1

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

 Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH = h dersek, hipotenüsBC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdırÜçgeni ve Uzunlukları Fazla bilinmeyen özel üçgenlerden birisi de üçgenidir Burada öklit kuralından üçgeninde 90 dereceden hipotenüse doğru çizilen dikÜÇGENİ Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir DAHA FAZLA BİLGİ İÇİN TIKLAYINIZ Powered by Create your

Dik Ucgen Vikipedi

Dar Acili Ucgen Nasil Cizilir On Www Clinicaveterinariamercedesgrande Es

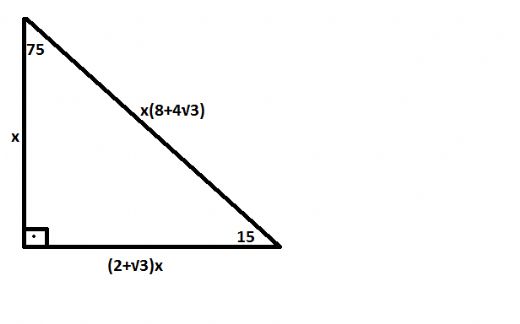
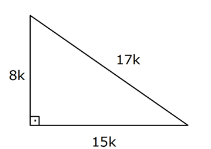
(8 – 15 – 17) Üçgeni Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir (7 – 24 – 25)Üçgeni Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır75 derece karşısındaki kenar = (2 kök 3)x 90 derece karışışındaki kenar = (8 4 kök 3) Bu şekilde yapılan işlem ile beraber 15 75 90(iii) () ÜÇGENİ Kenar uzunlukları () sayıları veya bunların katı olan bütün üçgenler dik üçgendir k R A B 15k C 8k 17k AB = AD = 10 br ABE üçgeni (15 75 90 ) üçgenidir ABE üçgeninde E nin AB ye en yakın uzaklığı hipote

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

1

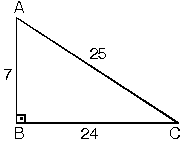
 Açılar böyleyken 15 75 90 üçgeninin kenar uzunlukları da şu şekilde olmalıdır BC kenarı 30 cm AB kenarı 25 cm AC kenarı 5 cm Geometri dersine çalışırken size yardımcı olacağını düşündüğümüz diğer konu anlatım yazılarımızı da okumayı unutmayın Altıgenin Alanı Nasıl Bulunur?1536 Merhabalar hocam, dik üçgende kenar uzunlukları verilmiş bana iç açılar soruluyor bunu nasıl hesaplayabilirim ? 15 75 90 Üçgeni Kuralı nedir?

Ozel Ucgenler

15 75 90 Ucgeni Webders Net

 Örnek Bir 15 75 90 üçgeni düşünelim;(A) açısı = 90 (B) açısı = 75 açısı = 15 açıları ise uzunlukları kurala şu şekilde olmak zorundadır (BC) = 30 cm (AB) = 25 cm (AC) = 5 cm olmak zorundadır 15 75 90 üçgeni özel kuralları yukarıda verildiği şekildedir Açılarını bilinmesiyle çok rahat uzunlukları da bilinmektedir Aynı şekilde 45 45 90 üçgeni, 15 75 90 üçgeni ve 30 30 1 üçgeni de önemli özel üçgenler arasındadır Bu yazıda biz 30 60 90 üçgenine odaklanacağız Yukarıdaki üçgende 30 60 90 üçgeninin kenar uzunlukları gösterilmiştir Kenarları karıştırmamak adına büyük açının karşısına uzun kenarın olduğunu

Top 12 75 90 Ucgeni En Iyi 22

3 4 5 Ucgeni Ve Ozellikleri Not Bu

Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olurOlmak üzere 4 tanedir Bu üçgenler, geometrinin bütün konularında soru içerisinde mutlaka gelmektedir Bu üçgenlerin özellikleri için okumaya devam edin Üçgeni üçgeni, kenar uzunlukları veya katları şeklinde olan üçgenlerdir Üçgeni 15 75 90 üçgeninin özelliği ise üçgenin hipotenüsüne ait yüksekliğin hipotenüsün uzunluğunun 1/4 'ü kadar olması olarak ifade edilebilir Bir örnek vermek gerekirse;

Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt

Ucgenler Alkan Hoca Matematik Yks Tyt Ays Kpss Ales Dgs Ygs Lys Teog

Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek,(5 12 13) Üçgeni Kenar uzunlukları (5 12 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir (10 24 26), (15 36 39), gibiKenar uzunlukları 8, 15, 17 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait(8 15 17) Üçgeni Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir 4 (7 24 25) (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır

Zel Genler 1 Dk Gen 2 Kzkenar Gen

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4 h olurÖzel üçgenler konu anlatımı matematik 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik Bu doğrultuda 15 derecenin karşısındaki kenar uzunluğuna, 'x' denirse, diğer kenarlar şu şekilde ele alınır;

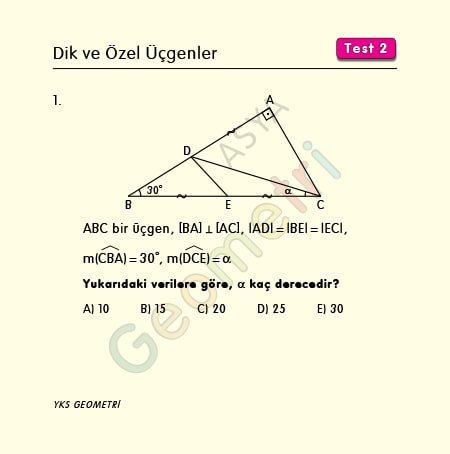
Dik Ve Ozel Ucgenler Test 2 Ders Geometri

Ozel Ucgenler Konu Notlari Www Matematikkolay Net Kenarlarina Gore Ozel Dik Ucgenler

 15 75 90 Üçgeninde Kenarların Oranı 15 75 90 üçgeninde kenarlar arasında belirli bir oran vardır Bu oranı ezbere bilmediğiniz taktirde kendiniz de elde edebilirsiniz Ancak elde etmekle vakit harcamak yerine doğrudan oranları ezberlemek de sizin tercihinizdir 15 75 90 üçgeninde 15'in karşısı 1 birimse 75'in karşısı √3 2 birim olur

15 75 90 Ucgeni Pow Bylge

30 60 90 Ucgeni Sorulari

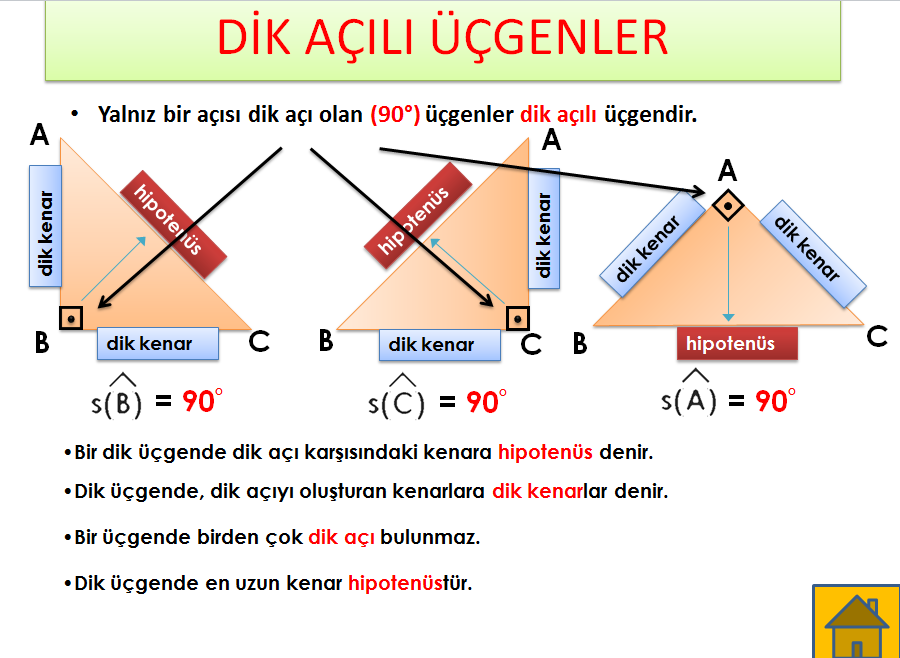
Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

Ozel Ucgenler Konu Anlatimi

Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt

Dik Ucgen Derspresso Com Tr

Genler Gen Etler Ekenar Gen Kzkenar Gen Dk

Almak Mendil Dusmanlik 90 15 75 Hvekorat Com

90 Derece 75 Derece 15 Derece Ucgeni Eodev Com

Dik Ucgende Trigonometri Bikifi

Maxresdefault Jpg

Ozel Ucgenler

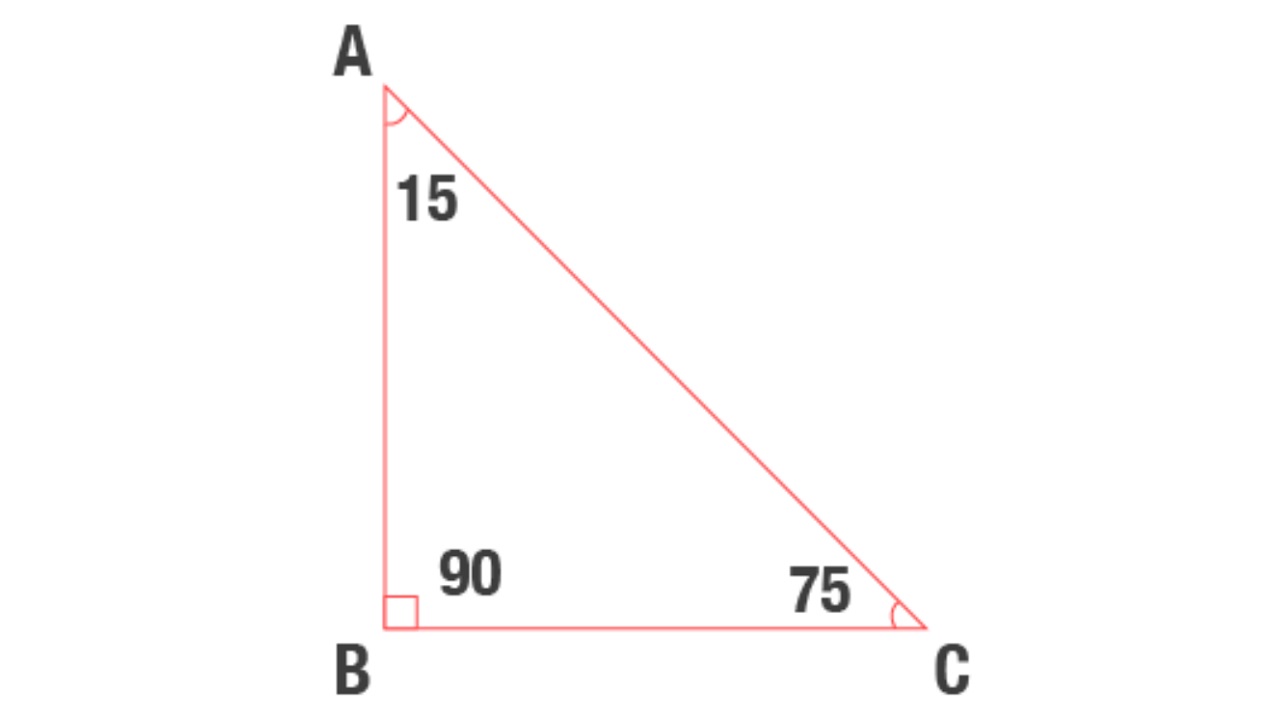
Ozel Ucgenler Nelerdir Ozellikleri

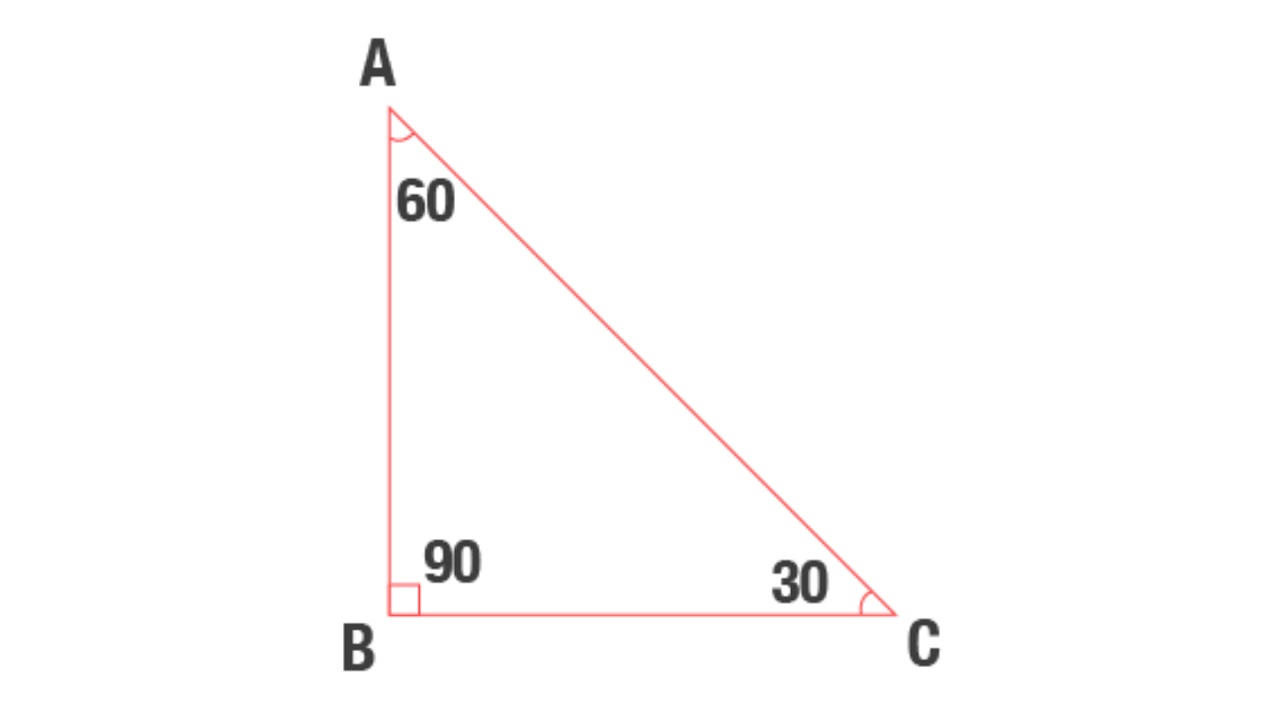
Ozel Ucgenler Nelerdir Ozellikleri

Net Fikir Ekim

Top 19 15 75 Ucgeni Formulu En Iyi 22

Ozel Ucgenler Konu Anlatimi Ozel Ucgenler Nelerdir Ogretmen Tercihim

Zel Genler 1 Dk Gen 2 Kzkenar Gen

Dik Ucgende Trigonometri Bikifi

Net Fikir Ekim

Ozel Ucgenler

Top 15 75 90 Ucgeni Kenarlari En Iyi 22

Top 19 5 7 8 Ozel Ucgeni En Iyi 22

Populer Icerik

Top 15 75 90 Ucgeninin Ozelligi En Iyi 22

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

Ozel Ucgenler Nelerdir Ozellikleri

1

Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz

Net Fikir Ekim

15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim

Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

90 75 15 Ucgeni Ozellikleri

15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri

15 75 90 Ucgeninin Ozellikleri Nelerdir

Zel Genler Dik Gen Zel Genler L L

Ozel Ucgenler Konu Anlatimi

Ozel Ucgenler Nelerdir Ozellikleri

Hususi Ucgenler Nedir Ozellikleri Hakanseyhan

3

Ozel Ucgenler Konu Anlatimi

Zel Genler 1 Dk Gen 2 Kzkenar Gen

Ppt Ozel Ucgenler Powerpoint Presentation Free Download Id

Acilarina Gore Ucgenler Ppt Indir

Almak Mendil Dusmanlik 90 15 75 Hvekorat Com

30 60 90 Ucgeni Ozellikleri

Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube

Dik Ucgen 15 75 90 Ucgeni Islemli Em Iyi Secicem Gereksiz Engellenir Eodev Com

15 75 90 Ucgeni Pow Bylge

Ozel Ucgenler Konu Anlatimi

Ozel Ucgenler

Dik Ucgen Vikipedi

15 75 90 Ucgeni Not Bu

Ozel Ucgenler Diyot Net Nedir

Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube

Murat Sen Akdeniz Universitesi Ucgenler Ppt Video Online Indir

Ozel Ucgenler Nelerdir 3 4 5 5 12 13 8 15 17 7 24 25 Ucgeni Ve Katlari Mmsrn Com Egitim Ve Bilgi Sitesi

Ucgenlerde Uzunluk Matematik Ve Geometri

1

Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir

15 75 90 Ucgeni Ozellikleri Ve Kurallari

15 75 90 Ucgeninin Ozellikleri Nelerdir

Th Q Eskenar Ucgen Alani

Ozel Ucgenler

Ozel Ucgenler Pdf

15 75 90 Ucgeni Not Bu

Ozel Ucgenler Konu Anlatimi

Ozel Ucgenler Nelerdir Ozellikleri

A Replica Record With Radius cm Turns Through A 1 Degree Angle How Far Does A Point On The Rim Travel Quora

Net Fikir

15 75 90 Ucgeni Kenar Bagintisi Ispat

15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz

30 60 90 Ucgeni Ve Ozellikleri Not Bu

15 75 90 Ucgeninin Ozellikleri Nelerdir

Incoming Term: 15 75 90 üçgeni kenar uzunlukları,