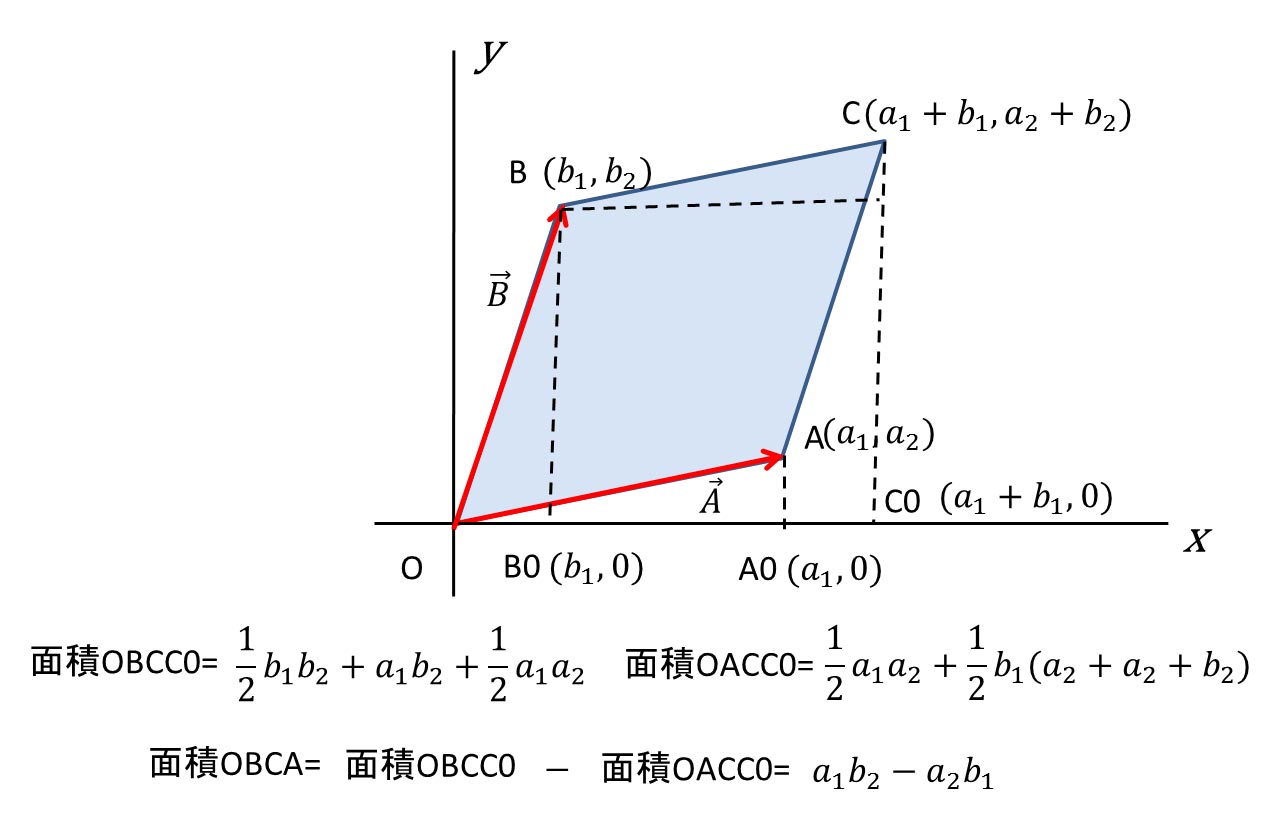
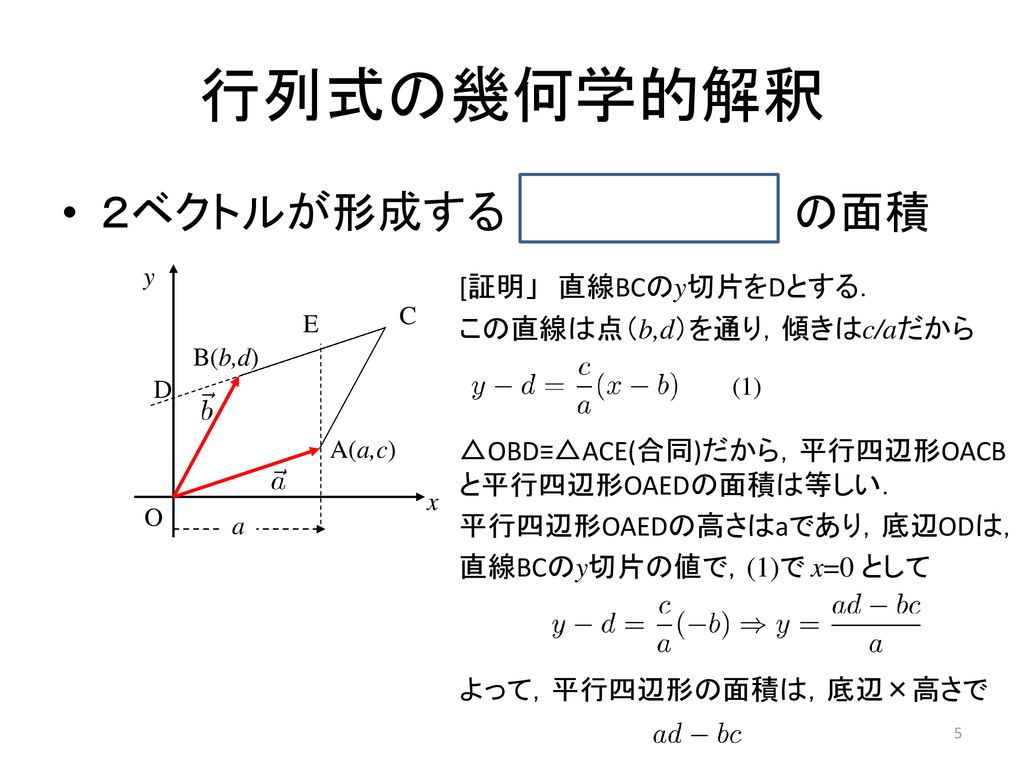
< 平面のベクトルと行列式> 原点を始点とする2つのベクトル a = ³ a1 a2 ´ ,b = ³ b1 b2 ´ に対して,原点O(0,0)と3点 A(a1,a2),B(b1,b2),C(a1 b1,a2 b2) をとると,四角形OACB は平行四辺形となる。 この平行四辺形の面積をS とする。aとbの位置関係が 図1のような場合 S = ¯ ¯ ¯スカラー三重積 まず,ベクトル は一次独立だとします.外積の定義より, は,長さがベクトル の張る平行四辺形の面積に等しく,向きは平行四辺形の法線方向を向いたベクトルです.(次図参照.外積の向きは右手系に取っています.)18年8月日(月)3次元空間で、2つのベクトルa,bを隣り合う2辺とする平行四辺形の面積Sを求めることを考えてみた。 ①ベクトルの内積のみを使って解く方法(高校数学)②ベクトルの外積を使う方法の2通りの方法を示した。 ②はS=|a×b|で求められる。 この公式は、①の方法を使って証明した。 ベクトルの外積について知識があると、やさしい問題となる
エクセルのグラフで学ぶ気象学 補説05
ベクトル 平行四辺形 面積 公式
ベクトル 平行四辺形 面積 公式-平行四辺形abcd において,2 つのベクトル = a , ad = b とすると,ベクトルの和 + は対角線ac で図示できる。 ベクトル ,の加法 + では,の終点を の始点に合わせると,の始点と の終点をつないだもつ平行四辺形を,この平行 6 面体の底面と考えると,この底面の面積 S はS = h となる。 また,図13 に示すように,aとhのなす角φが,0 ≦φ π をみたすとき, a cos φは,a の終点から底面に下した垂線の長さ,つまり平行 6 面体 の高さl を表すことになる
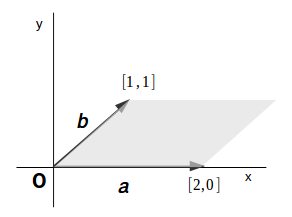



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門
成分表示されたベクトルの内積公式の導出 — 双線形性を用いた "展開" によって基本ベクトル同士の内積に帰着する;ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで平行四辺形の面積 の公式 検定教科書では必須ではないが非常に便利 または大学数学でこのようなc をa, b のベクトル積または外積といい、 (32) c = a×b と表す。 注意31 ベクトルa, b の外積a×b を用いて、 • ベクトルa, b が作る平行四辺形の面積を計算することが出来る。 • ベクトルa, b に垂直なベクトルを求めることが出来る。
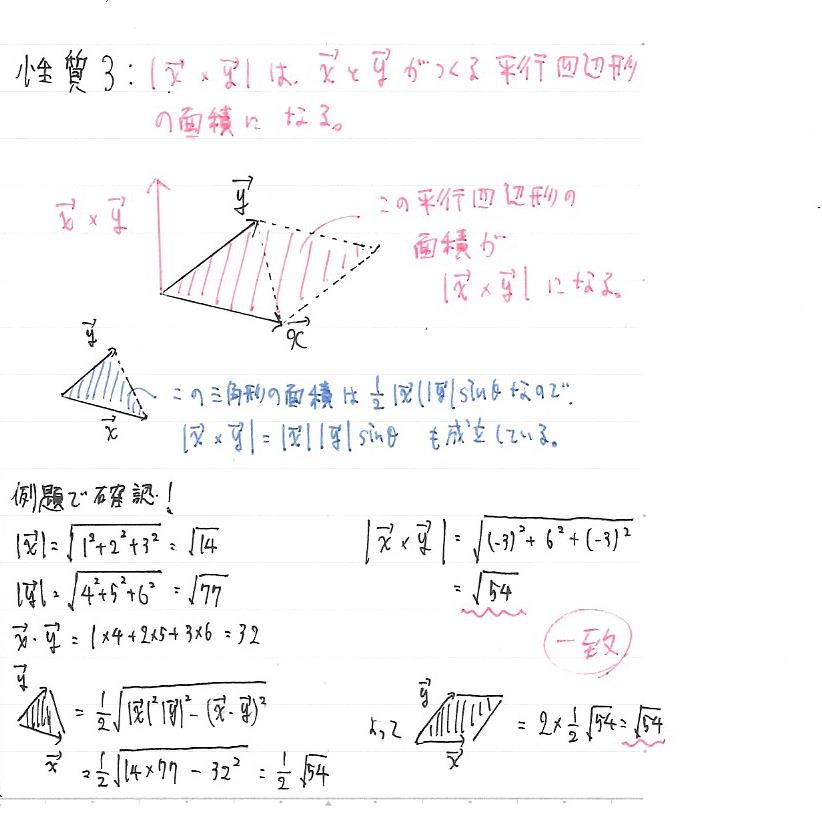
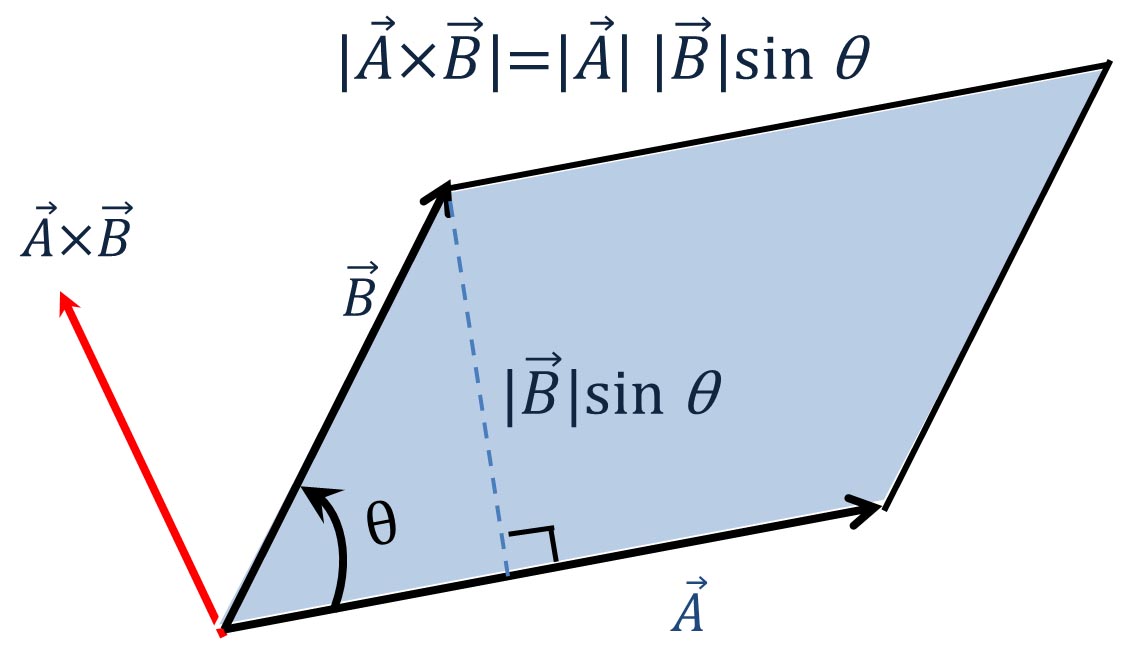
平行四辺形の面積 まず, 2つのベクトル(ベクトルを横に書く悪習は辞めましょう) が張る平行四辺形の面積を考えよう 小学生でも習うこの公式 = (底辺) × (高さ) を思い出そう 底辺をとすると, これに対する高さは となる ここで, はとがなす角である すると, 面積は となる 上の議論 から明らかなように、 2つのベクトル a a と b b によって構成される平行四辺形の面積 S S は 外積のノルムに等しく、 すなわち、 S = ∥a×b∥ S = ‖ a × b ‖ であり、 一方で、 S S は底辺×高さに等しい。 すなわち、 S =∥a∥∥b∥sinθ S = ‖ a ‖ ‖ b ‖ sin平面の法線ベクトル a&b& の長さは、平行四辺形の面積 u S に等しい b & a & S ab && u a,b & が作る平行四辺形を含む面に 垂直で、長さが1のベクトルを法線ベク トルといい、 a b a b S a b
線形性を用いることで 幾何的な問題を代数的に扱ってしまえる のが "線形性のマジック" 平行四辺形の面積と2次行列式 平行四辺形も同様の公式で求められる 三角形の面積の公式の確認 三角形 O A B OAB O A B において, ∠ A O B = θ \angle AOB = \theta ∠ A OB = θ とすると,三角形 O A B OAB O A B の面積 S S S は, S = 1 2 ∥ a undefined ∥ ∥ b undefined ∥ sin θ S = \dfrac{1}{2}\\overrightarrow{a}\\\overrightarrow{b}\\sin\theta S = 2 1 ∥ a ∥∥ b ∥ sin θ で表されまA =(a1,a2), b =(b1,b2)が作る平行四辺形の面積S はS = a1b2 −a2b1 である。 G27 直線のベクトル方程式 直線 l が 2 点 A, B を通るとき, 2 点 A, B の位置ベクトルを a =




平行四辺形の面積の求め方 公式と計算例




平行四辺形 対角線 長さ 計算
空間の平行四辺形の面積を求めるには下記のようにベクトルを使えば簡潔な公式で表せられます。 参考文献 基礎数学1 線型代数入門 齋藤正彦 (著) 東京大学出版会 しかし、成分表示にしようと思うと、とてつない数の項 (225項)が出てきて 手書きで計算1 ベクトルの基礎 6/14 B A A B B A u A B A Bsin 図16 ベクトルの外積 平行四辺形の面積 は図16に示す2つのベクトルのなす角度である.方向を表すuは単位ベクトルで,ベク トルAを Bの方に向かって回したときに,右ネジの進む方向と定義する.ベクトルの大き さは,右図のようにベクトルAと Bが作 ベクトル 平行 四辺 形 面積 ベクトルを用いた三角形・平行四辺形の面積の公式と求め方|高校生向け受験応援メディア「受験のミカタ」 ベクトル 平行 四辺 形 面積 「外積の長さ = 平行四辺形の面積」 証明



ベクトルの外積をマスターしよう オンライン受講 東大に 完全 特化 東大合格 敬天塾




平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori
ベクトルの外積と平行四辺形の面積 身勝手な主張 For more 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで平行四辺形の面積 の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間外積の大きさ = 平行四辺形の面積 外積の大きさ(長さ)は、 外積を構成するベクトルが成す平行四辺形の面積に等しい。 すなわち、 四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。




勉強しよう数学 三角形の面積をベクトルで分解して計算する
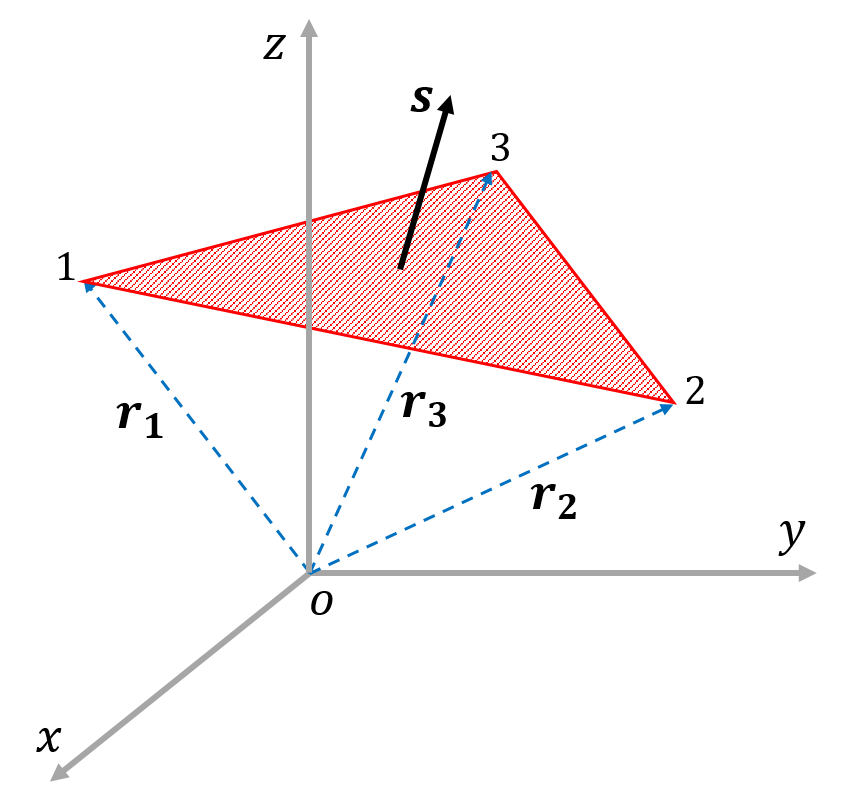



三角形の面積 科学技術計算ツール
補足 平面ベクトルa,b が(面積が0 でない) 平行四辺形を作るとする a からb まで正の向きに測った角をθ (後の ために ´ π {2 ă θ ő 3 π {2) とし , a を正の向きに π {2 だけ回転させたベクトルを ra "ベクトルの外積 の向きは,ベクトル の向きからベクトル の向きへ右ネジを回転させたとき,ネジの進む向きとする. ベクトルの外積 の大きさは, によってできる平行四辺形の面積に等しいものとする.したがって,平行四辺形の面積の公式はこの場合も成り立つのである. 上の操作をよく観察すると,次のことがわかる. 平行四辺形を長方形に変形するには, 平行四辺形をいくつかの線分で切り分けて, 各部分を平行移動すればよい




高校数学b ベクトルの成分表示と平行四辺形 受験の月



空間ベクトル平行四辺形の三つの頂点がa 2 1 3 b 1 Yahoo 知恵袋
平行四辺形の面積 まず, 2つのベクトル ベクトルを横に書く悪習は辞めましょう が張る平行四辺形の面積 を考えよう 平行四辺形 abcd がある。 違う位置にあっても、「向き」と「大きさ」が同じであれば、同じベクトルであるとされます。で形成される平行四辺形の面積は、x a y b -x b y a で表される。 とくにaとbの位置関係によって、絶対値内の正負を下図のように決定できる。 ※この公式は、以下のような図からも導けます。 ベクトルの向きによって、いろいろな形になりますが、すべて四角形の面積(4辺と対角の和から) たまたま訪れました。 この公式は,S=absin (θ1)÷2cdsin (θ2)÷2 と比較して,誤差が小さくなるのだろうか。 対角の距離を測定する手間が省けて非常に助かります。 助かりました! アンケートにご協力頂き有り難う




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




高校数学b 平行四辺形とベクトル 例題編 映像授業のtry It トライイット
また平行四辺形OAGDの面積と長方形OAG'D'の面積は等しい。つまり が成り立つ。 このときπ平面上のベクトルの方向に関して であることが言える。 このことと、||:||=OB':OC' であることを考慮すると、平行四辺形OB'D'C'と平四辺形OHJIは互いに平行四辺形の面積は (底辺 \(w\)) \(\times\) (高さ \(h\)) で求められます。 ベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) を平行でない二辺とする平行四辺形を考えます。それらのなす角は \(\theta\) とします。 すると底辺 \(w\) は、ベクトル \(\overrightarrow{a}\) の大きさ \(\ \overrightarrow{a} \\) です。つくる平行四辺形の面積Sに等しい。又a×b の向きはaからbに,向かって回転するとき に,右ねじの進む方向である。従ってb × a はその反対向きであり b× a = −(a ×b) が成り立つ。(図1) 3つのベクトルa,b,cが図2のような位置
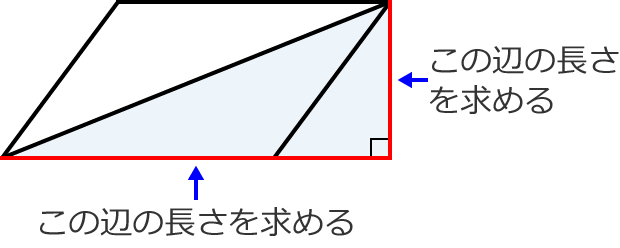



平行四辺形の対角線の長さの求め方




ねこ騙し数学
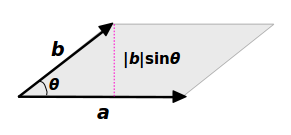
平行四辺形面積計算機 オンラインの平行四辺形の面積計算機は、その底面と高さに基づいて平行四辺形の面積を見つけるのに役立ちます。 平行四辺形面積の式 以下は、平行四辺形の面積の計算式です。四辺形の面積⃗a⃗bsinθ(θ はベクトル⃗aと⃗bの間に角)に等しい。(2) 方向と向きは、ベクトル⃗aと⃗bとに垂直で⃗aから⃗bへ右ネジを廻すときに ネジの進む方向。 その時に、次の分配法則等が成り立つ。 (1)⃗a×⃗b = −⃗b×⃗a,⃗a×⃗a = 0 (2)⃗a×(⃗b⃗c) =⃗a×⃗b⃗a×⃗c外積の大きさ 外積のベクトルの大きさ a → × b → は a → b → sin θ となり, a → と b → を2辺とする平行四辺形OADBの面積に相当する. 平行四辺形OADBの底辺OAの長さは a → ,高さBHは三角形OBHの三角比より b → sin θ となる. よって,平行四辺形の面積 S は, ページトップ




ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門




エクセルのグラフで学ぶ気象学 補説05
ベクトル 平行 四辺 形 面積。 ベクトルの外積の定義、図形的な意味、微分の公式 位置ベクトルの公式一覧 位置ベクトルについては「」の記事で詳しく解説しているので,ぜひチェックしてください。 成分計算で定義すれば、4次元ベクトルの角度を想像 下の2つのベクトル \( \vec{a} \), \( \vec{b} \) で張られる平行四辺形があるとします。 平行四辺形の面積は、底辺 OA × 高さ BH で求めることができますね。 底辺は \( \vec{a} \)、高さは \( \vec{b} \sin \theta \) となるので、平行四辺形の面積 \( S \) は\




勉強しよう数学 三角形の面積をベクトルで分解して計算する



1



ベクトル平行四辺形証明 位置ベクトルを利用して平行四辺形を Yahoo 知恵袋



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門



2つのベクトルが作る平行四辺形の面積は その2つのベクトルの外積 Yahoo 知恵袋




外積を使って解く入試問題例 東大落ちの受験勉強法




物理のための数学 ベクトルの外積 お茶処やまと屋



Http Msec Kumamoto U Ac Jp Problem Pdf Linear 1 14 Ans Ex L1 14 1 Ans Pdf




勉強しよう数学3c エディントンのイプシロンと行列式とベクトルの外積
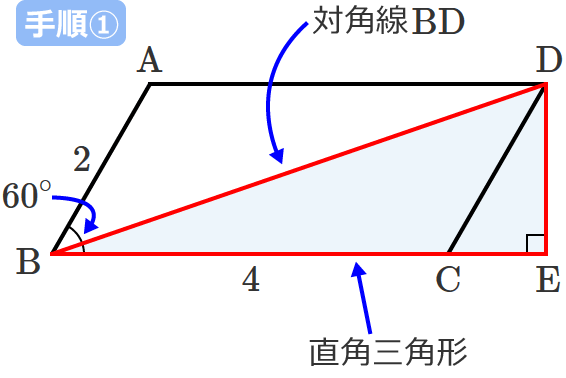



平行四辺形の対角線の長さの求め方




平行四辺形の面積を求めるある問題について 身勝手な主張
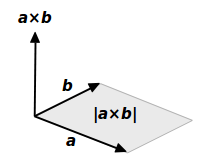



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門
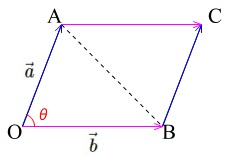



ベクトルの大きさと内積だけで表す面積の公式




平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clear
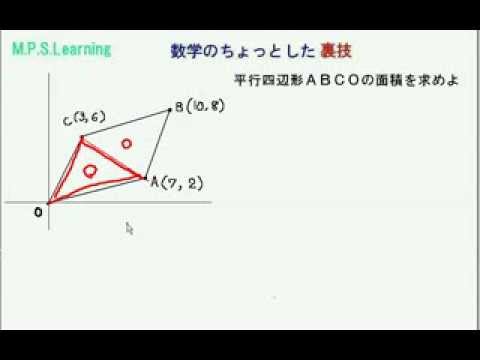



1次関数の応用 平行四辺形の面積 Youtube




勉強しよう数学 ひし形の対角線の直交の公式と2重平行四辺形の面積の公式



Studydoctor空間座標と平行四辺形 数b Studydoctor
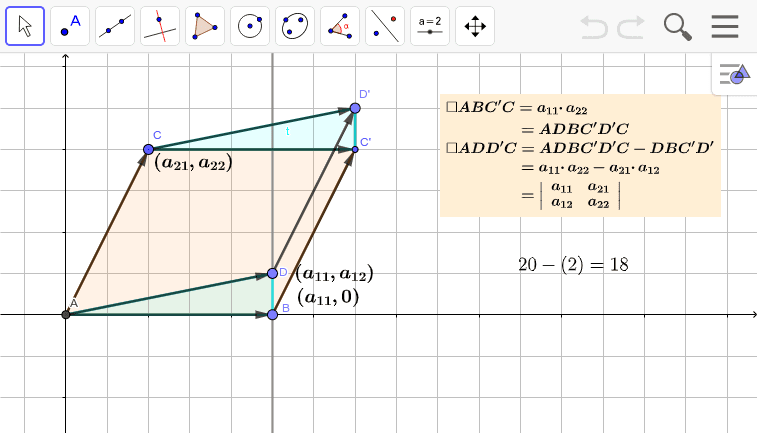



平行四辺形の面積と行列式 Geogebra




外積の長さ 平行四辺形の面積 証明 理数アラカルト




高校数学 平行四辺形の面積の求め方 練習編 映像授業のtry It トライイット



平行性変形でのベクトルの小手技




線形代数 試行錯誤
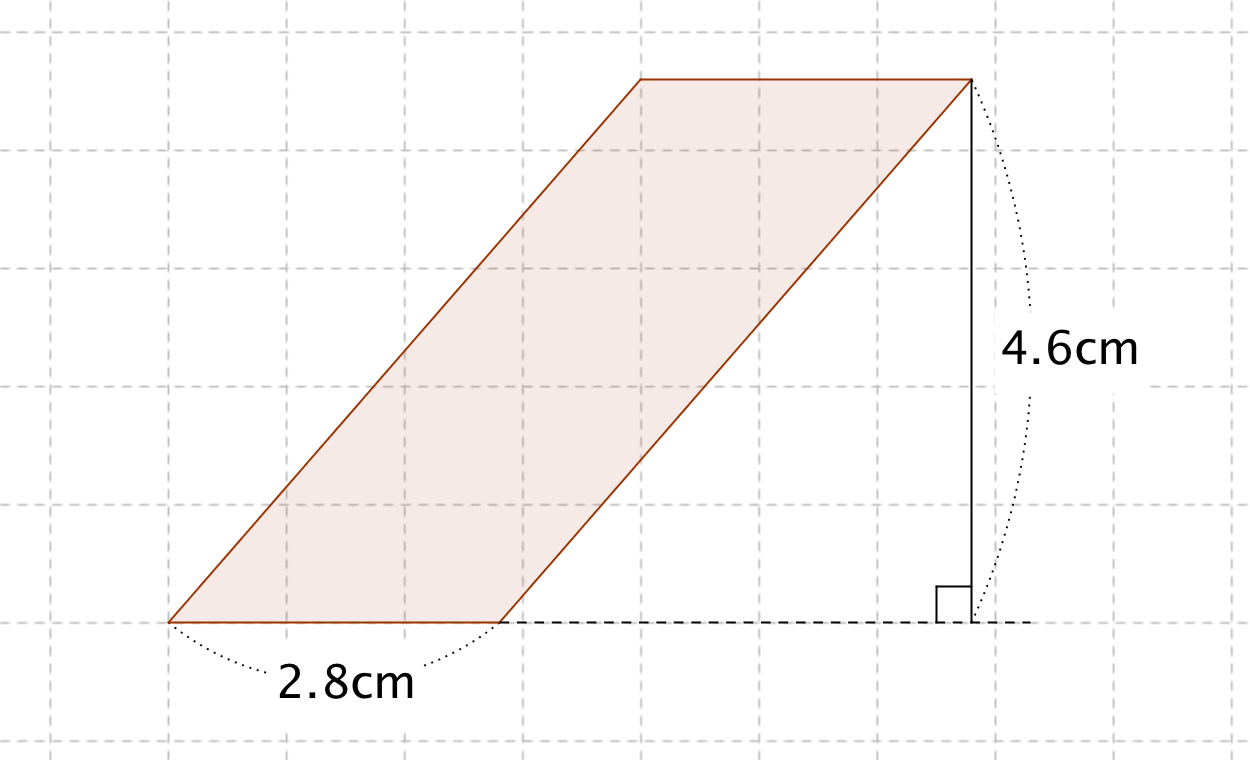



平行四辺形の面積の公式 算数の公式



ベクトルによる平行四辺形の条件 大学受験の王道




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




外積の定義と性質 ベクトル代数 1 大学生 専門学校生 社会人 数学のノート Clear




外積の長さ 平行四辺形の面積 証明 理数アラカルト




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



なぜ ベクトルの外積の長さが 平行四辺形の面積に等しいのでしょうか A Yahoo 知恵袋



エクセルのグラフで学ぶ気象学 補説05




2次の正方行列式と平行四辺形の面積 機械学習に詳しくなりたいブログ
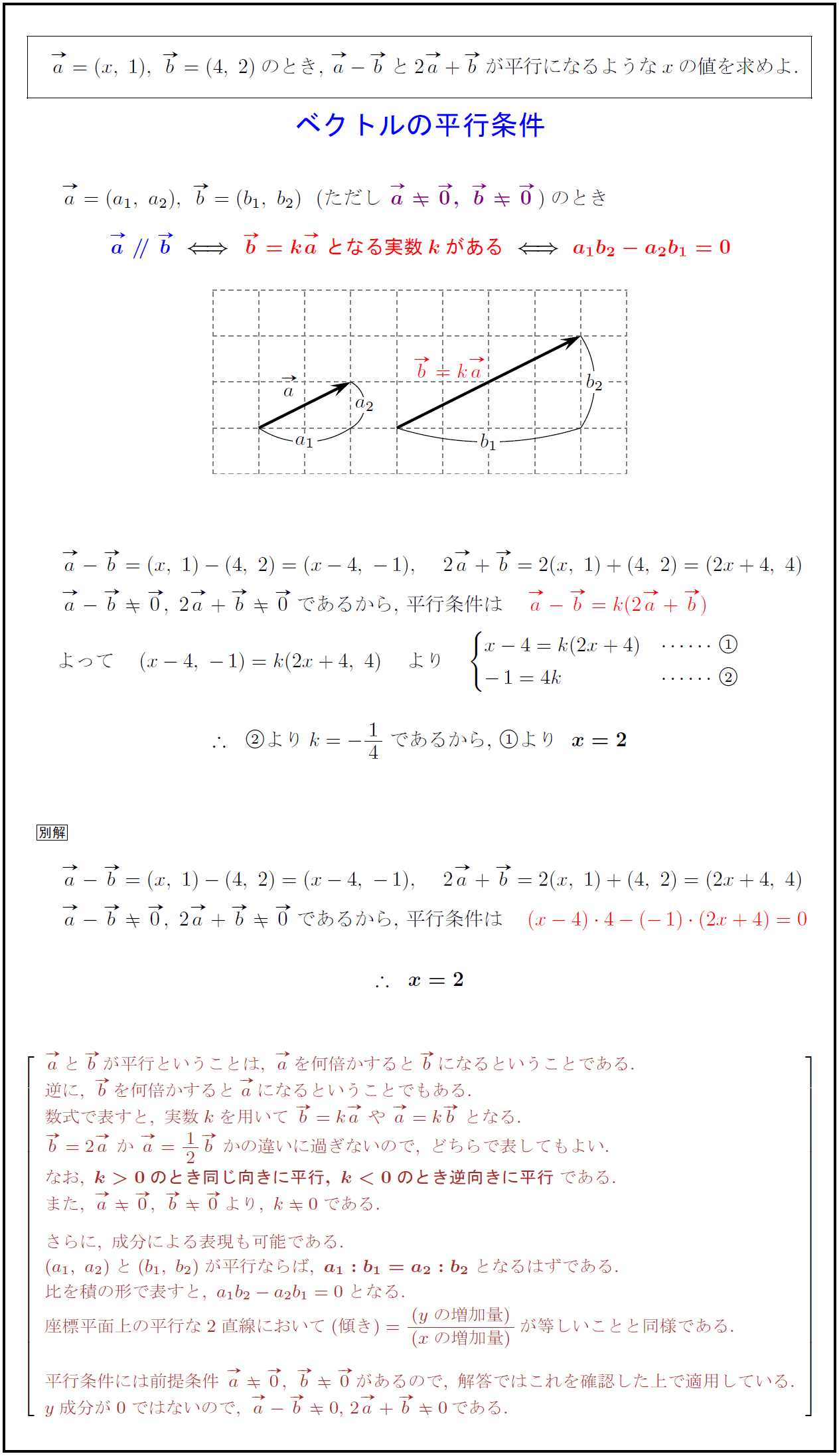



高校数学b ベクトルの成分表示と平行条件 受験の月




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積の求め方 公式と計算例




ベクトルの外積と平行四辺形の面積 身勝手な主張




高校数学b 平行六面体と空間ベクトルの演算 受験の月



ベクトルの内積 スカラー積 と外積 ベクトル積 の成分表示




ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門




勉強しよう数学 2重平行四辺形の面積の公式



1



平行四辺形の面積の2等分
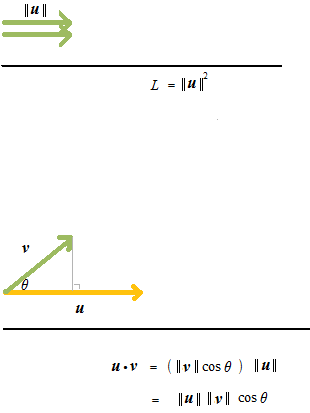



621 ベクトル 内積 外積 Tokyomaths Com



1



ベクトルの平行条件 垂直条件とは 内積公式や証明 計算問題 受験辞典




平行四辺形のベクトル 面積比の問題です 大学入試数学問題の解説 解答




1 Dfrac92 Descubre Como Resolverlo En Qanda




8月 13 試行錯誤



ベクトル方程式とは 図形別の公式 直線 円 や問題の解き方 受験辞典




標準 平行四辺形とベクトルの演算 なかけんの数学ノート
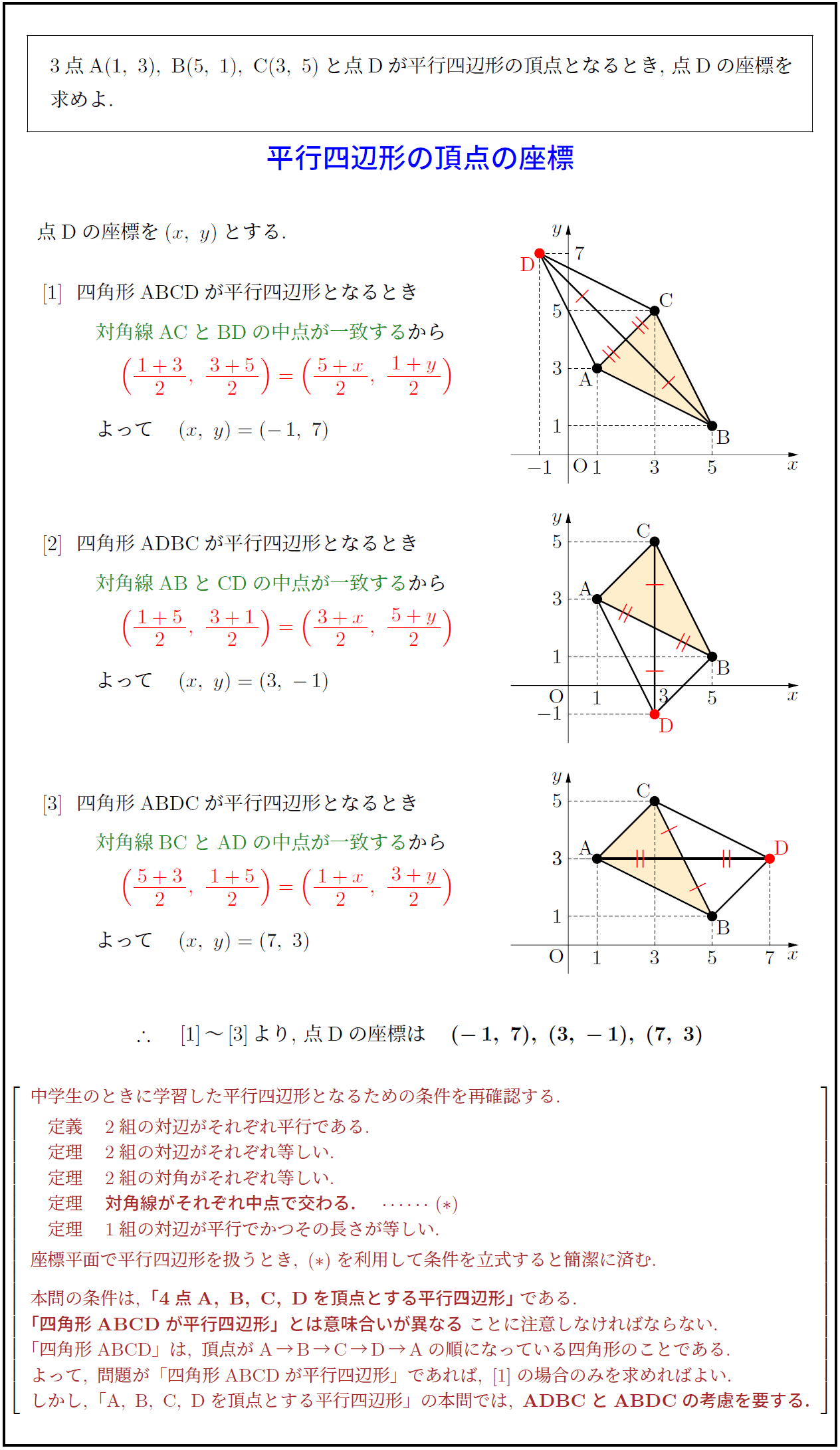



高校数学 平行四辺形の頂点の座標 受験の月



曲線座標表示の一般論への補足その2 平行四辺形の面積とベクトル外積 Jo3krpの独り言




勉強しよう数学 三角形の面積をベクトルで分解して計算する



平面幾何におけるベクトル演算 内積と外積
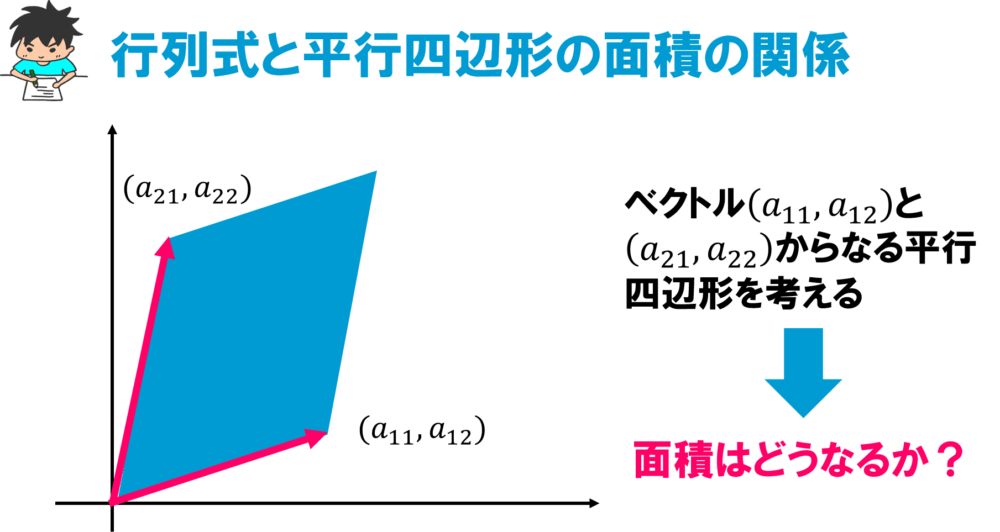



行列式の計算方法と図形的意味を解説してみる 線形代数を宇宙一わかりやすく解説してみるサイト




倍横距法を用いて多角形の面積を求める方法




簡単公式 平行四辺形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




空間における平行四辺形の面積 外積 1 231頁 高卒で大学数学



面積分



数学iiic ベクトルの 外積 あるいは平行四辺形の面積




ベクトル 怜悧玲瓏 高校数学を天空から俯瞰する




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題



Excelを使った数値計算ツールsuitexl
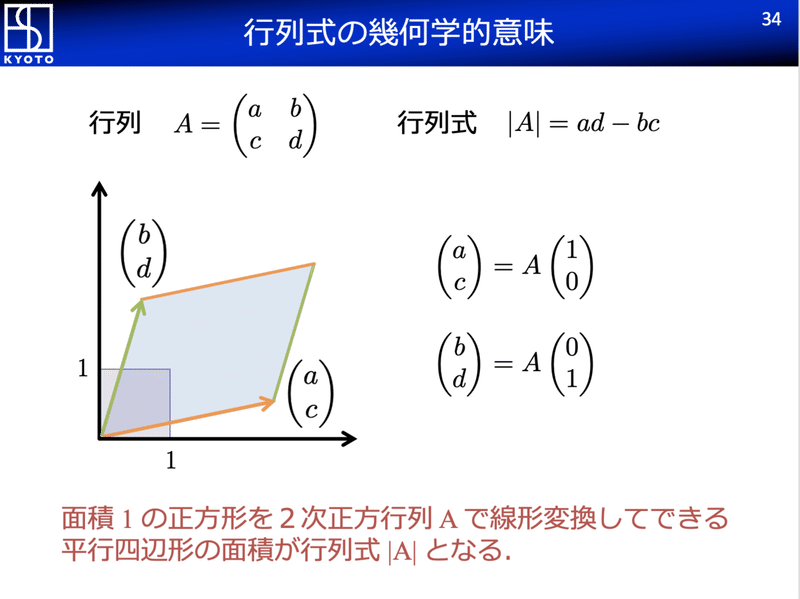



行列式 A Ad の幾何学的意味 Dr Kano Note
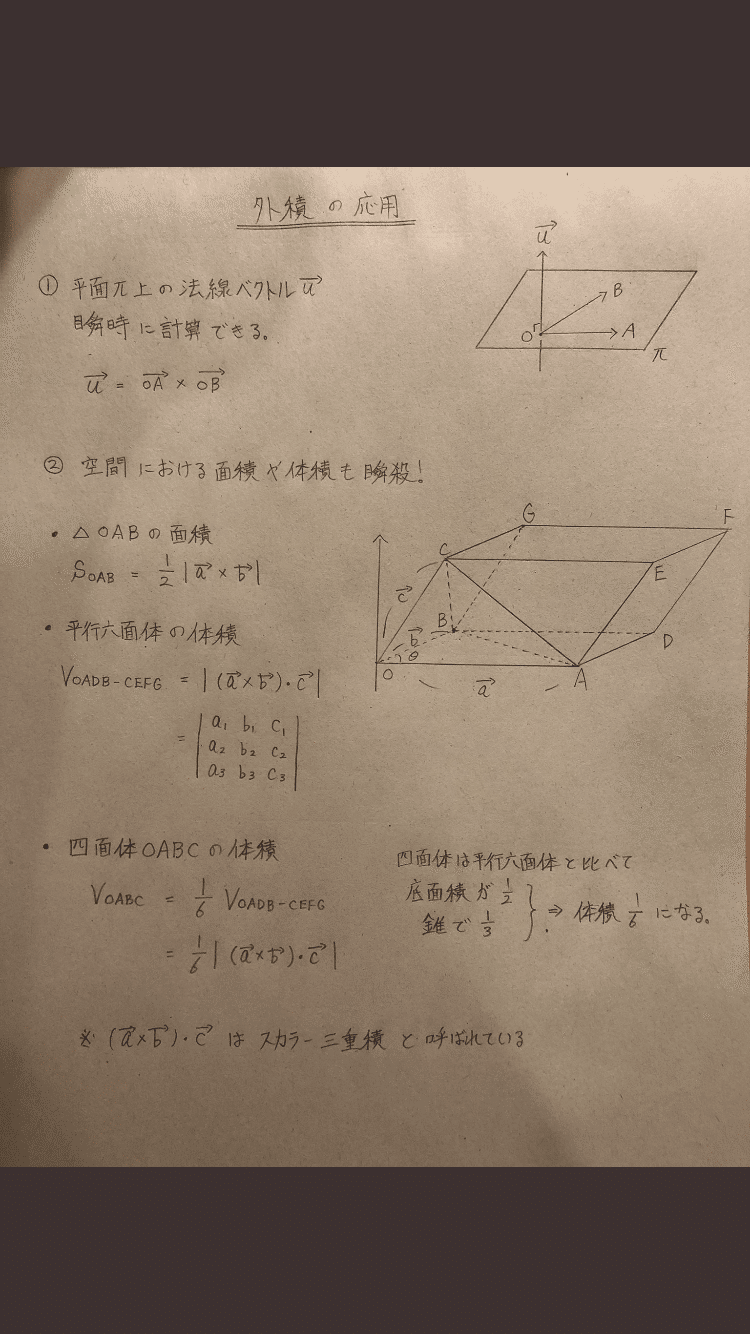



空間の幾何学 解法まとめ 数検1級対策 Note




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
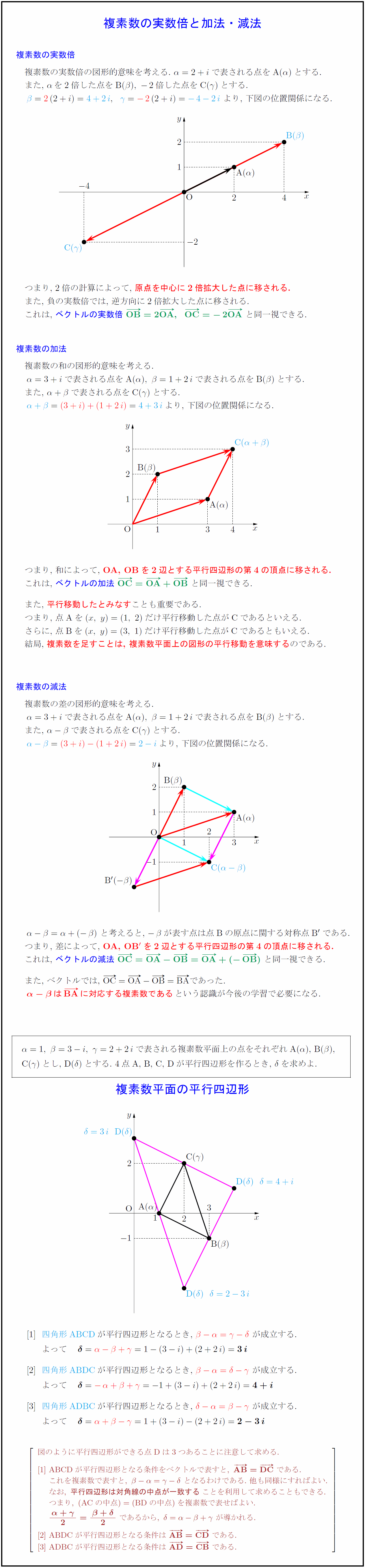



高校数学 複素数の実数倍と加法 減法 複素数平面の平行四辺形 受験の月




新訂版序文の人 大類昌俊 外出連続39日目 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで 平行四辺形の面積の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間ベクトル を学ぶ時の初等的な




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学



2
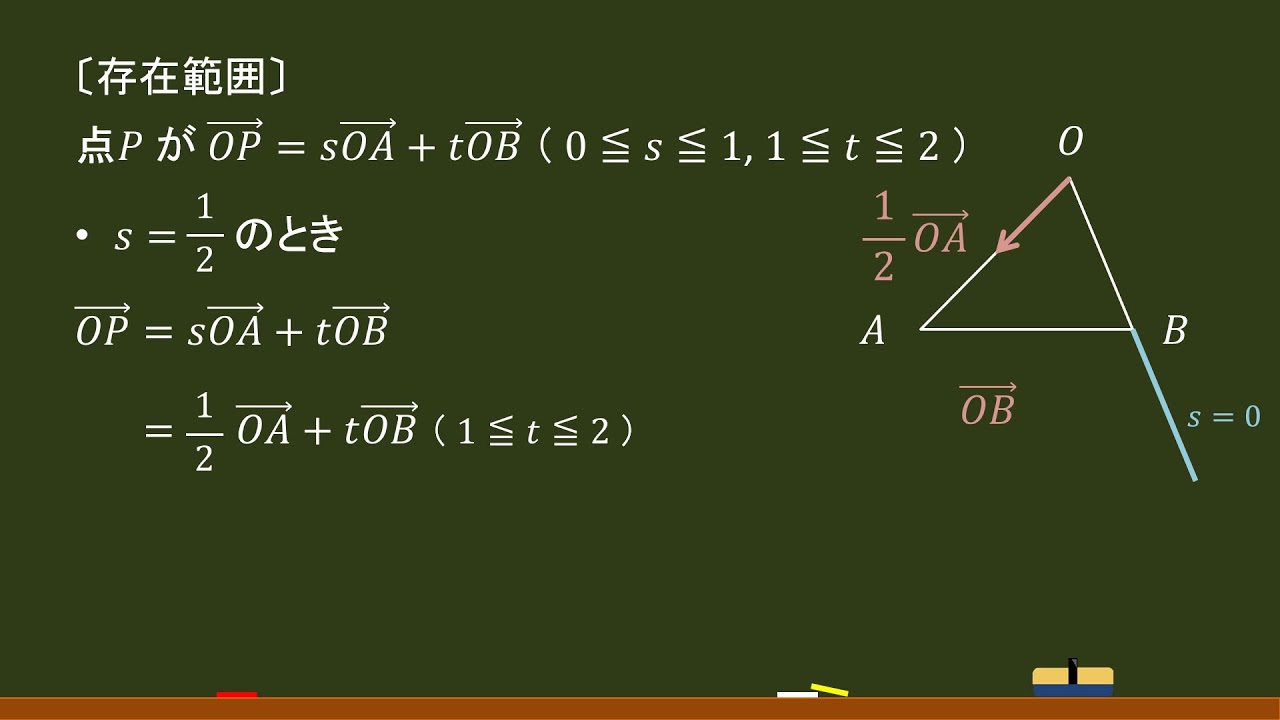



平面ベクトル 点の存在範囲 平行四辺形タイプ オンライン無料塾 ターンナップ Youtube



数学b ベクトルの範囲です 平行四辺形abcdの辺cdを3 1に内分する Yahoo 知恵袋



3



行列式 方程式の解 Cramerの公式 余因数展開 Ppt Download




2014年 東大数学 理系第1問の解説 三角関数 ベクトル 外積 解と係数の関係 オンライン受講 東大に 完全 特化 東大合格 敬天塾




数学と音楽 年度岐阜大学文理共通数学2番 数学b ベクトルと平行四辺形の面積比 学習村の 国公立へ行こう




外積の長さ 平行四辺形の面積 証明 理数アラカルト




8月 13 試行錯誤
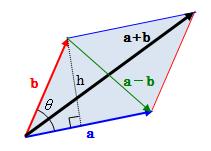



技術計算製作所 ベクトル解析 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Science Math Vector




新訂版序文の人 大類昌俊 外出連続39日目 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで 平行四辺形の面積の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間ベクトル を学ぶ時の初等的な



行列式 線型代数 数学教育




3 の平行四辺形の面積の求め方を教えてください 答えです 42 Clear




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ



Fn Vector3d Crossproduct メソッド Flash テクニカルノート




ベクトル三重積と平行六面体及び四面体の体積 身勝手な主張




ベクトルの外積と平行四辺形の面積 身勝手な主張




平行四辺形の面積 S Ad の証明2つ Youtube




1 1 A Dfrac23 B I Descubre Como Resolverlo En Qanda
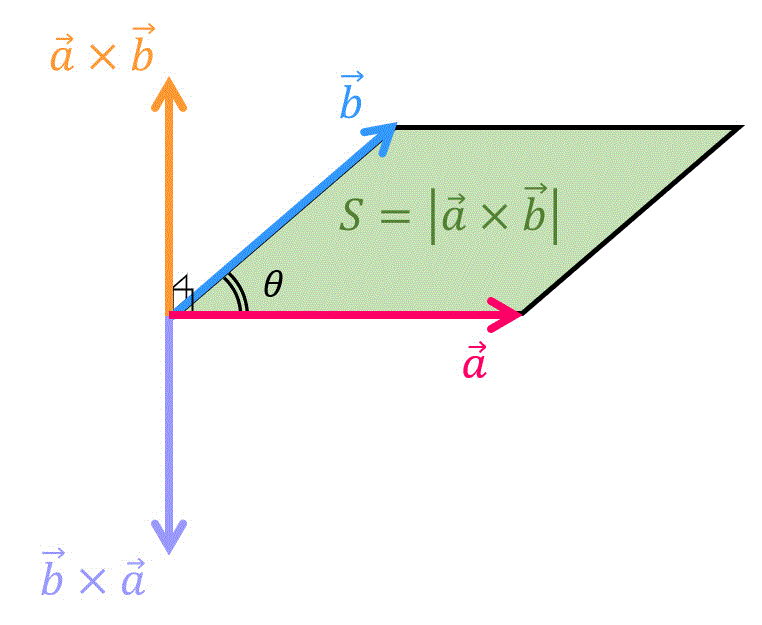



うさぎでもわかる線形代数 補充1 線形代数におけるベクトル 内積と外積 工業大学生ももやまのうさぎ塾




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積と行列式 Youtube



0 件のコメント:
コメントを投稿