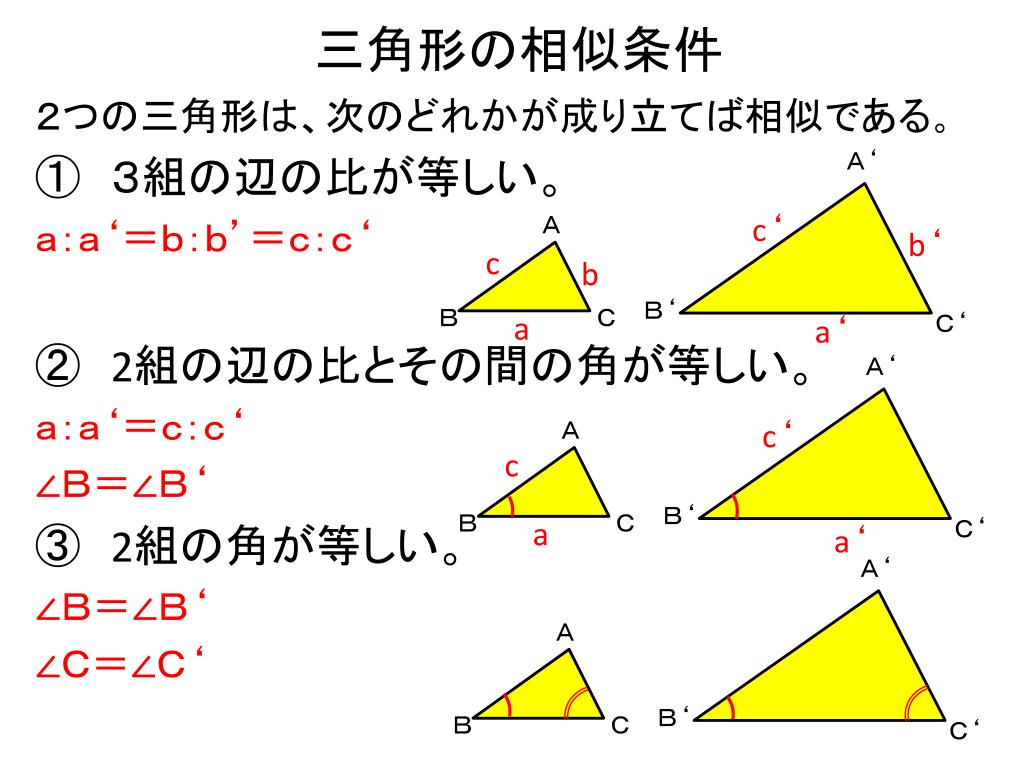
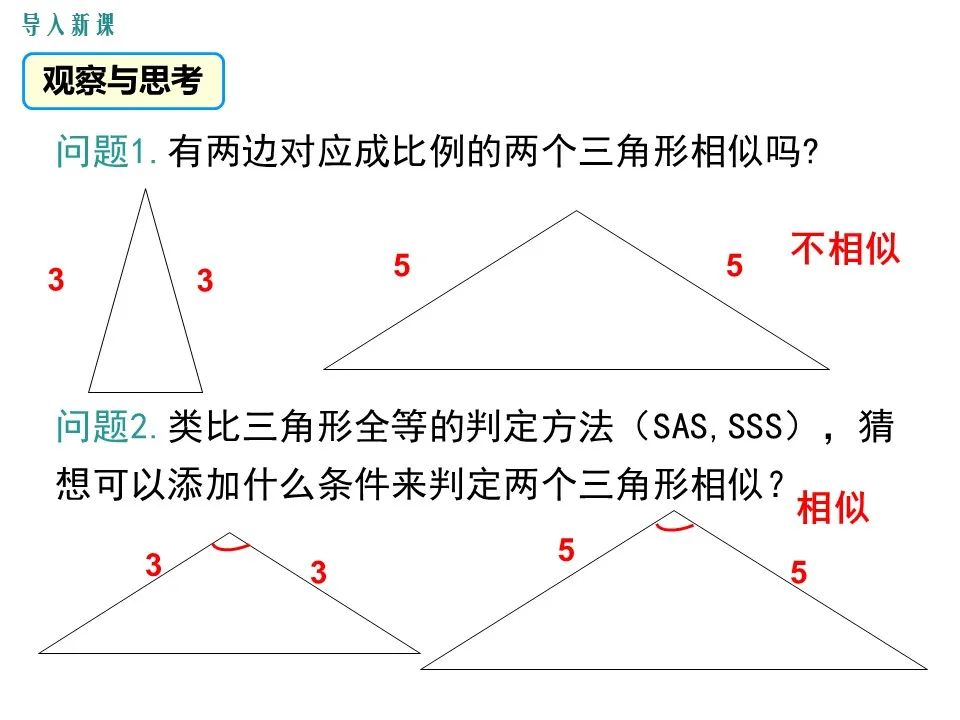
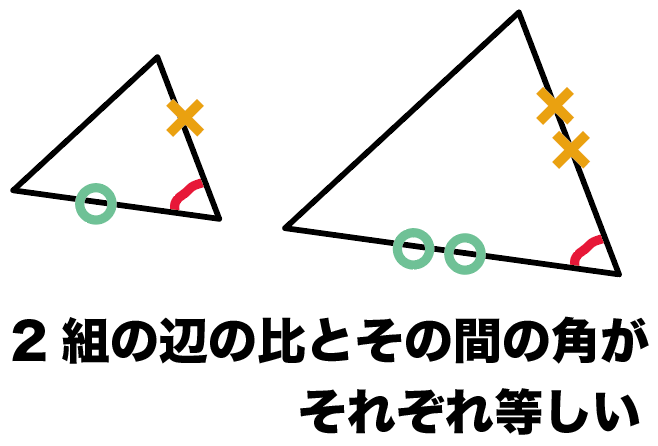
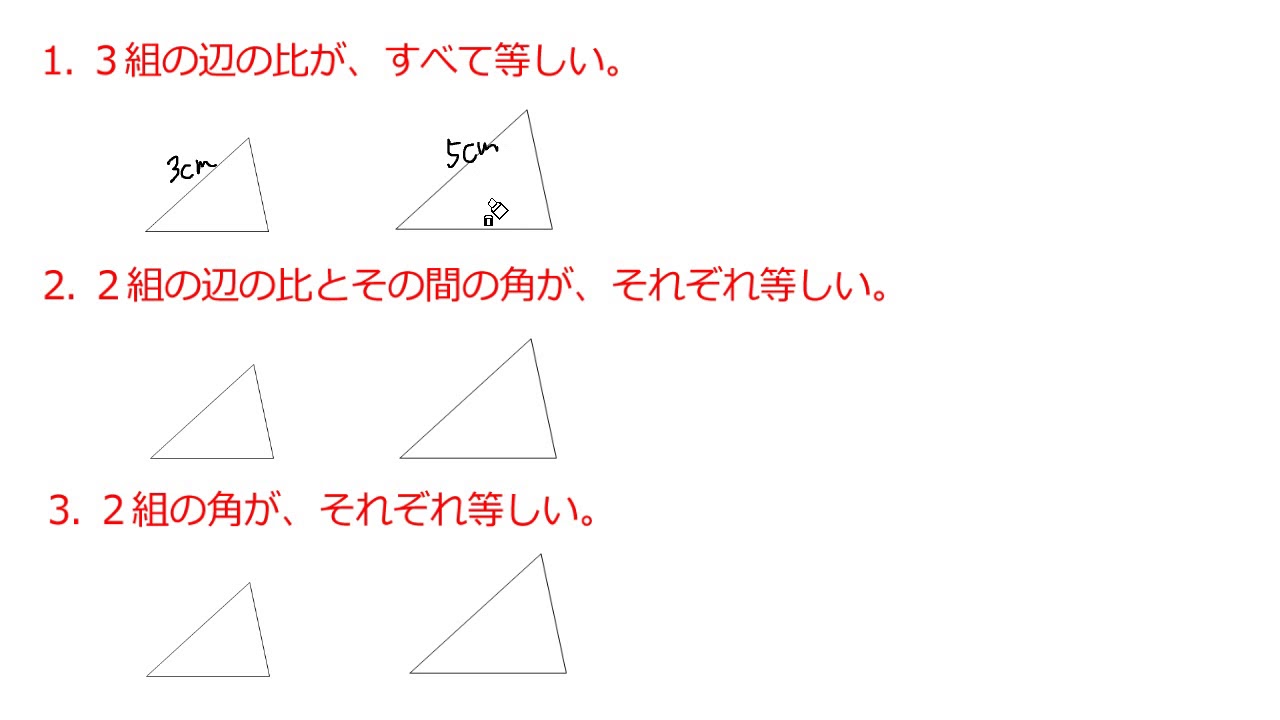
三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、 「2組の辺の比とその間の角が等しい」 という条件です。 個人的には一番使う回数が多いと感じました三角形相似的判定定理如下: 1)角角即两个角对应相等即可 2)边角边即两个边对应成比例,其夹角对应相等即可 3)边边边即三边分别对应成比例即可 4)直角三角形hl即一个直角边和一个斜边分别对应成比例即可 其它的如平行线截得三角形相似,则为判定三角形の相似条件 三角形の相似を証明するためには、「相似条件」というものを使います。 相似条件には、以下の \(3\) つがあります。 相似条件①3 組の辺の比がそれぞれ等しい \(3\) 辺の比がそれぞれ等しければ、相似と言えます。

02 相似三角形的性质 相似三角形的定理与圆幂定理高中数学 Youtube
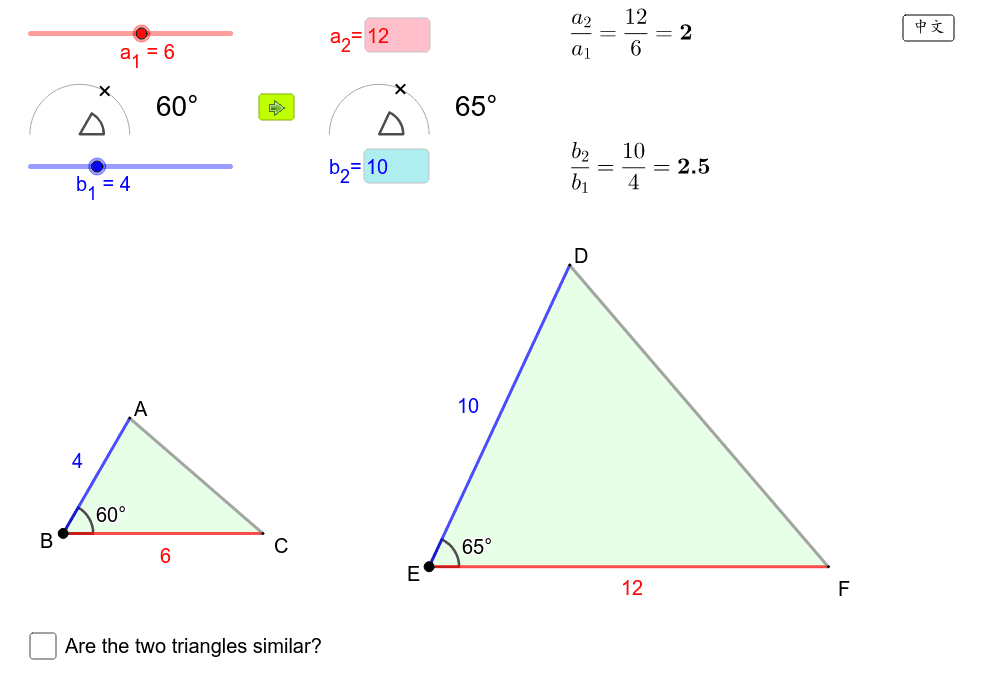
三角形相似条件
三角形相似条件-相似な三角形をかくにはどのような条件が必要だろうか? 一年生平面図形の三角形の作図で学んだことを覚えているかな? ①3辺の長さ ②2辺の長さとその間の角の大きさ ③1辺とその両端の角の大きさ この3つのいずれかがわかれば三角形を作図することができたんだ。 相似な三角形を作るにはなにがわかっていればいいかこれをもとに考えると ①3辺の長さ三角形の相似条件 \(2\) つの三角形があり、それらが相似であるかどうかを判定する。 そのために、三角形の相似条件があります。 相似条件 \(3\) 組の辺の比がそれぞれ等しい \(2\) 組の辺の比とその間の角がそれ
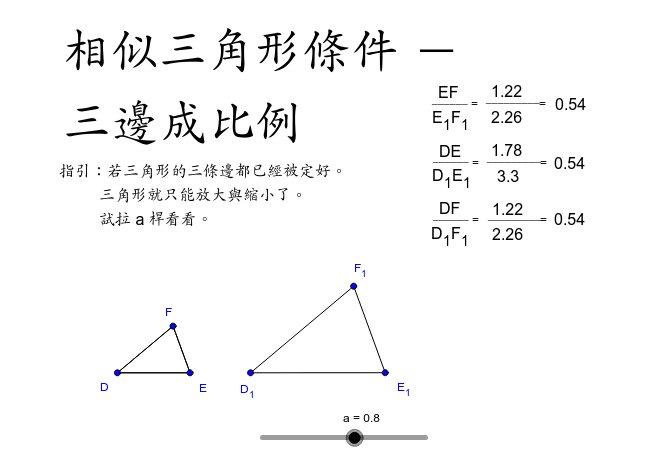



相似三角形條件 三邊成比例 Geogebra
三角形の相似条件 三角形の相似条件 とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。 2組の角がそれぞれ等しい。 このページの続きでは、三角形の図を見ながら、これらの相似条件判断两个三角形相似不仅需要测量很多边角大小, 还要经历计算 能否借助其中更少的条件就能判断两个三角形相似, 就是本节课的学习任务 设计意图:通过利用多边形相似定义证明三角形相似, 让学生切身感受到寻求更加简便的方法是有意义的この3つの中から相似な図形を見つけるときに 情報が少ない図形は、相似条件に当てはめることができません。 なので、情報が多く揃っている ABCと ABDが相似になるだろうな、と予想して この2つの三角形が、相似条件に当てはまるかを確かめていきます
相似三角形的条件 (二) 一、学生知识状况分析 学生知识技能基础: 学生的知识技能基础:学生在七年级下册第五章《三角形》里,已学习过三角形的基础知识 掌握了基本的概念; 在本章前面几节课三角形の相似が成り立つ条件③:2組の辺の比と間の角が等しい 2組の辺の比が等しく、その間の角が等しい ときも相似が成り立ちます。 まとめると以下の3つが三角形の相似条件です。 2組の角が等しい;证明三角形相似有三种方法: (1)两三角形中有两组角对应相等 (2)两三角形中有一组角对应相等,夹这两个相等角的两组边对应成比例 (3)两三角形三组边都对应成比例
つまり,三角形の相似条件は, 3辺 がそれぞれ等しい→ 3組の辺の比 がすべて等しい 2辺 とその間の角がそれぞれ等しい→ 2組の辺の比 とその間の角がそれぞれ等しい 1辺 とその両端の角がそれぞれ等しい→2組の角がそれぞれ等しい となります。 3の拡大・縮小と相似 三角形の相似条件 拡大・縮小と相似 三角形の相似条件Q1 三角形の相似条件として、正しくないものを選びましょう。 3組の辺の比がそれぞれ等しい。 2組の辺の長さとその間の角が




三角形の相似条件 On Vimeo




相似三角形定理的证明
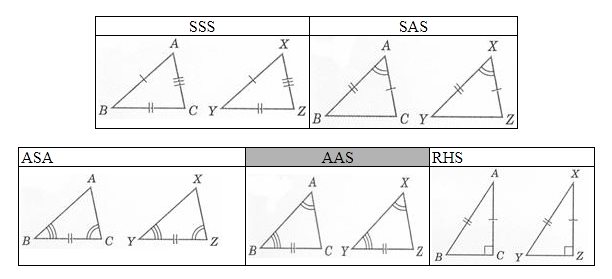
2 三角形の相似条件 2つの三角形は,次の各場合に相似である。 (ア)3組の辺の比がすべて等しいとき (イ)2組の辺の比とその間の角がそれぞれ等しいとき (ウ)2組の角がそれぞれ等しいとき 内容を式で表すと (ア)a:d=b:e=c:f (イ)a:d=b:e,∠C =∠F (ウ)∠B =∠E ,∠C =∠F もちろん上記以外の組み合わせでも相似となる (イ)a:d=c:f,∠B =∠E b:e=c:f,∠A三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」がなくなったものです。 ではこの三角形の相似条件をどのように使うのか、実際に問題を解きながら見ていき三角形相似条件、证明 一、判断三角形相似(与全等的对比) 相似三角形定义:三角分别相等,三边成比例的两个三角形 全等(特殊的相似) 相似 asa 两角对应相等的两个三角形相似 aas sas 两边对应成比例,且夹角相等的两个三角形相似 sss 对应边成比例的两个三角形相似 hl 直角三角形中,斜边与



1



解读相似三角形经典图形 科学猫
三角形の相似条件 知識・技能の習得と数学的な思考力・判断力・表現力の育成を目指します! 数学的活動を取り入れた授業展開案 単元「図形と相似」の小単元「三角形の相似条件」(2時間)における数学的活動を取り入れた授業展開案です。 単元 図形と相似 (啓林館) 1 図形と相似 ・2・ 三角形の相似条件 全2時間 1/2時OEは2つの三角形に共通な辺 よって3組の辺が等しいので 合同な図形の対応する角は 等しいので 2等分線になる なぜ、この作図が角の二等分線になるのだろう? D C B o A E動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




02 相似三角形的性质 相似三角形的定理与圆幂定理高中数学 Youtube



初中数学 相似三角形 全等三角形 腾讯新闻
両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3三角形の相似条件 三角形の相似条件 2つの三角形は次の各場合に相似である。 1 3組の辺の比が、すべて等しいとき 2 2組の辺の比とその間の角が、それぞれ等しいとき 3 2組の角が、それぞれ等しい多角形 相似条件 初等幾何学における多辺形(たへんけい、英 polylateral)または多角形(たかっけい、英 polygon;



三角形相似 三角形全等判定模型 初中数学几何重难点归纳 哔哩哔哩 Bilibili




数学 中3 44 三角形の相似条件 Youtube
2 相似条件のひとつに「 2 組の角がそれぞれ等しい」があります。 この条件で、なぜ2つの三角形が「相似」であることが言えるのか、その理由を説明しなさい。 相似③三角形の相似条件d 学 年 3年 学習日: 月 日( ) 中学校数学 3b5-3d三角形の相似条件 中3数学 証明問題で最も出題されるのがこの相似の証明です。 使う相似条件は99%「2組の角がそれぞれ等しい」と言って過言ではありません。 とにかく等しい角を2つ見つけることを心がけてください。4 三角形の合同条件を基にして、三角 ・①3辺の比を等しくかいた。 三角形の合同条件をより見方・考え方 形の相似条件を見いだしてまとめ 相似の性質をとらえ、 ②2辺の比とその間の角を等しくかいた。 どころにして、相似条件 る。




50 素晴らしい数学相似条件 最高のぬりえ




极客数学帮小课堂 相似三角形讲解
多角形に対しては,相似な図形の性質は相似であることの必要十分条件になっている.すなわち演繹的には導いていない. 23 三角形の相似条件 学校数学では,相似な図形の性質を認めた上で,三角形の相似条件を学習する.そし三角形相似的判定条件 两角对应相等,两个三角形相似;两边对应成比例且夹角相等,两个三角形相似;三边对应成比例,两个三角形相似;三边对应平行,两个三角形相似;斜边与直角边对应成比例,两个直角三角形相似;全等三角形相似。 1如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。 (简叙为:两角对应相等,两个三角形三角形形成的条件 1、如果三角形的两边分别为3和5,那么连结这个三角形三边中点所得的三角形的周长可能是() a 5 5b、5c.45d.4 2、等腰三角形的两边长分别为3和6,则这个等腰三角形的
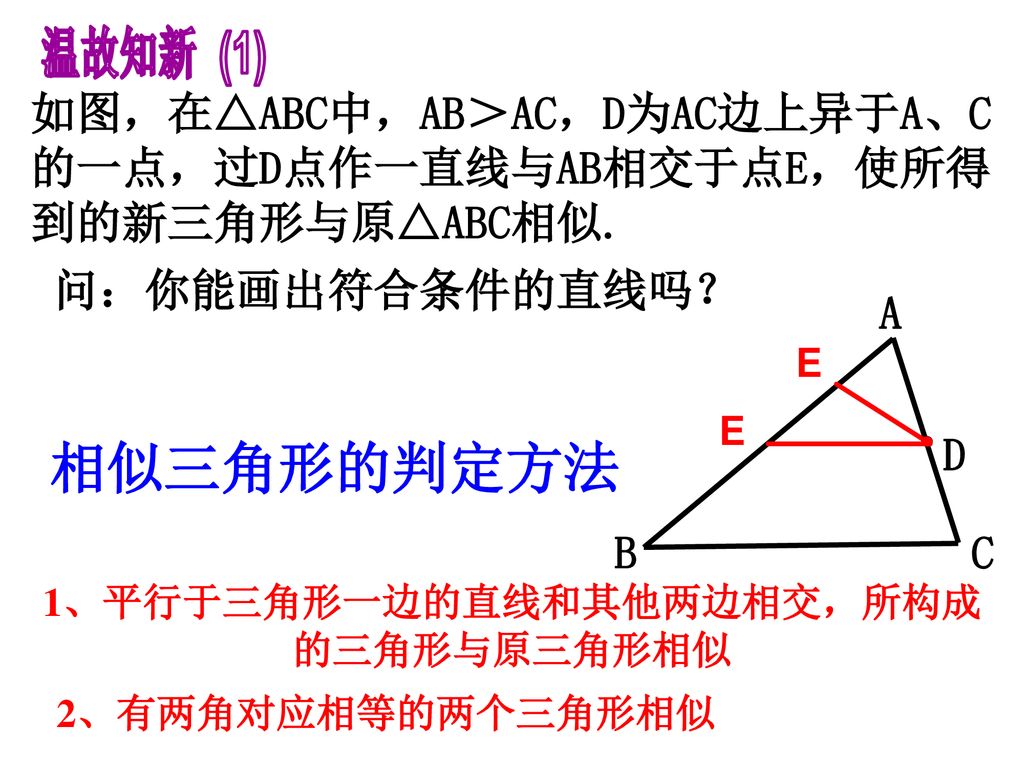



1 平行于三角形一边的直线和其他两边相交 所构成的三角形与原三角形相似 Ppt Download



教学反思 为什么判定相似不能用 边边角 腾讯网




50 素晴らしい数学相似条件 最高のぬりえ



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



相似三角形测试题不会做 极客名师为你解惑




6 4 探索三角形相似的条件 初中电子课本



三角形相似条件 腾讯视频
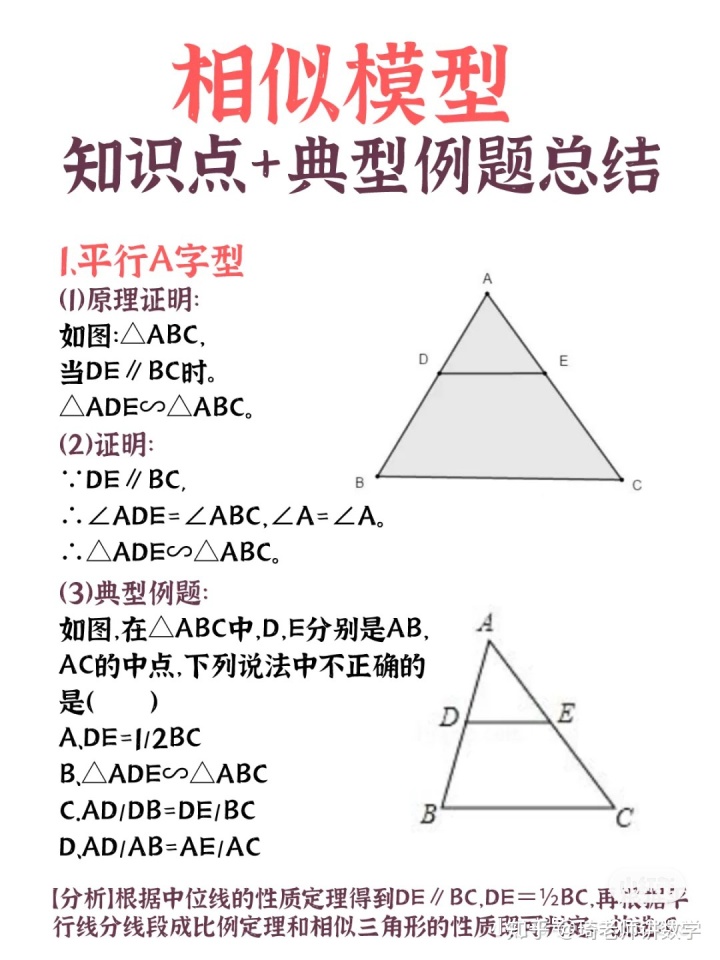



平行相似定理 初中数学 相似三角形模型合集提分收藏 阿诬123的博客 Csdn博客




1x版九年级数学下册6 4探索三角形相似的条件5导学案新版苏科版下载 Word模板 爱问共享资料




相似三角形的动点问题题型下载 Word模板 爱问共享资料



探索三角形相似的条件 图形的相似ppt 第2课时 第一ppt



相似三角形初中数学教案 初中数学教案 中国教育资源网



这道初中几何题条件少 一些学生不知所措 解题关键是相似三角形 几何题 三角形 初中 新浪新闻



初中数学相似三角形



探索三角形相似的条件 1 松鼠文库



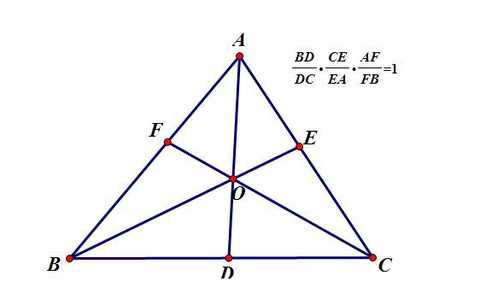
相似三角形 维基百科 自由的百科全书



相似三角形中的辅助线 学生版 教师版 沃文网wodocx Com



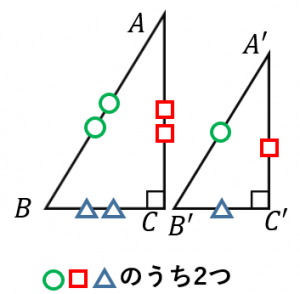
相似三角形 知乎



直角三角形の相似条件 具体例で学ぶ数学




三角形の相似条件
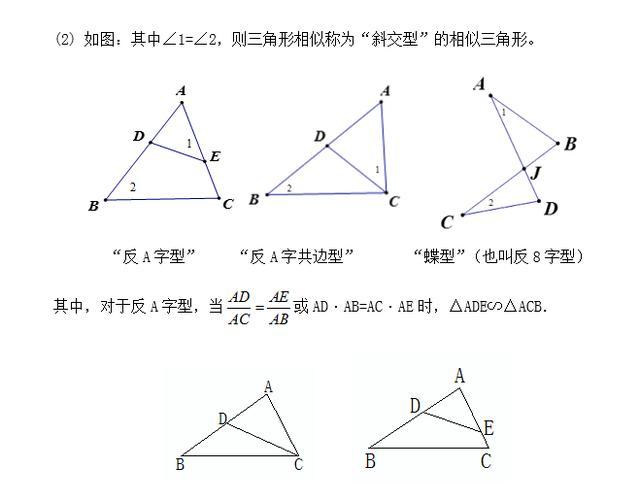



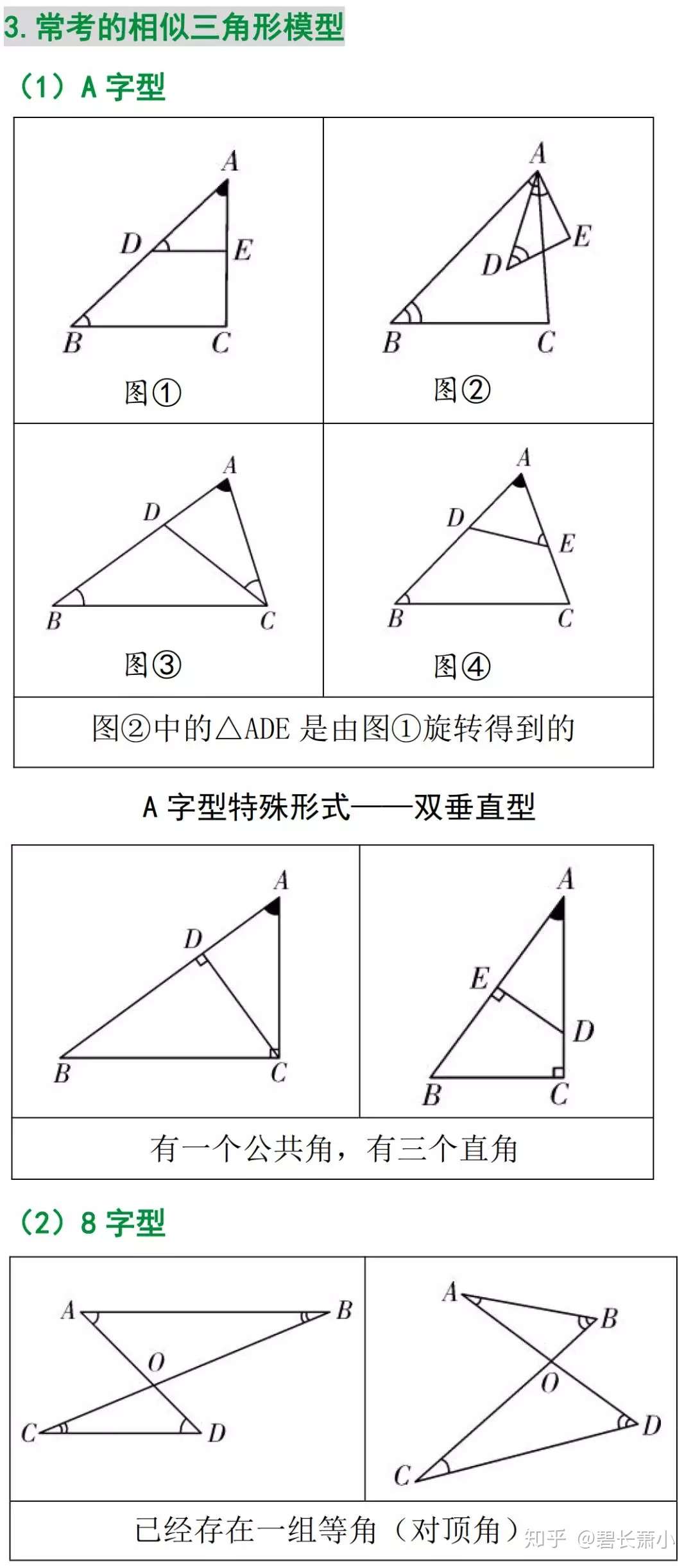
中考数学丨压轴题攻略必备 相似三角形的6大模型总结 知乎




75 数学相似条件 最高のぬりえ




一道高难度的经典几何题 知道考查相似三角形 但就是证不出来 线段 正三角形 代数 代数和 网易订阅




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




八年级数学下册10 4探索三角形相似的条件 2 同步练习苏科版下载 Word模板 爱问共享资料




三角形の相似条件 修正 On Vimeo



03相似三角形的判定图形的相似初中数学初三 Youtube



1




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題




相似三角形 中的基本图形及其解答技巧与口诀 每日头条



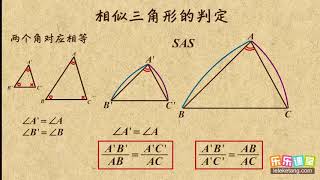
Ppt 相似条件と証明 Powerpoint Presentation Free Download Id




相似三角形條件 三邊成比例 Geogebra




八年级数学10 4探索三角形相似的条件 4 下载 Word模板 爱问共享资料



初中一线三等角 强相似模型傻傻分不清 原来只差一个条件




全等三角形 维基百科 自由的百科全书




4 5相似三角形判定定理的证明课件 七七文库www 77wenku Com
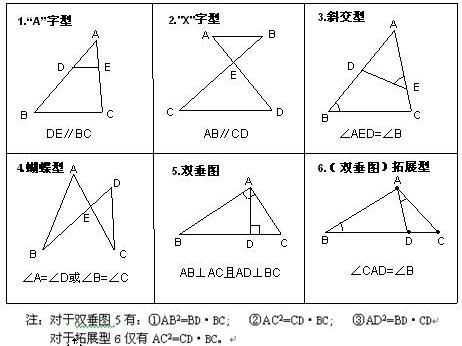



相似形 搜狗百科



相似三角形的判定



教学反思 为什么判定相似不能用 边边角 腾讯网



1




探索三角形相似的条件 图形的相似ppt课件 Ppt课件下载 人人ppt




75 数学相似条件 最高のぬりえ




觀念 三角形的相似性質 Youtube



最新相似三角形测试题 松鼠文库
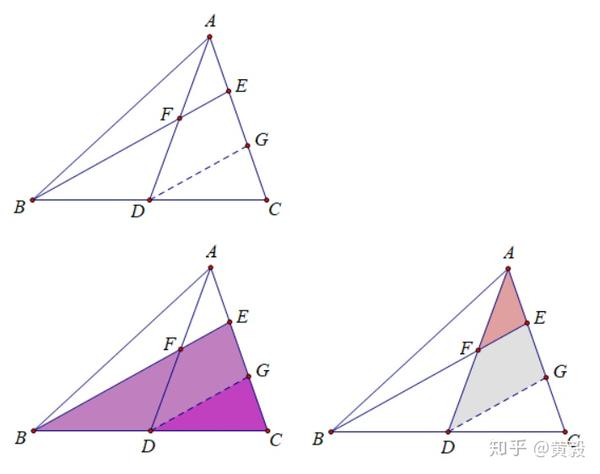



利用平行线构造相似三角形 用这道题来训练效果最好 知乎
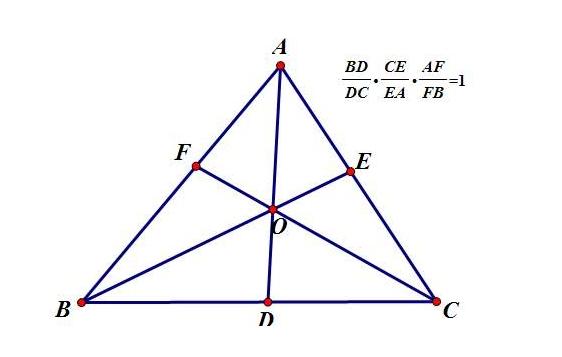



9 6 相似三角形 知乎




浙教版九上4 3两个三角形相似的条件 1 教案下载 Word模板 爱问共享资料
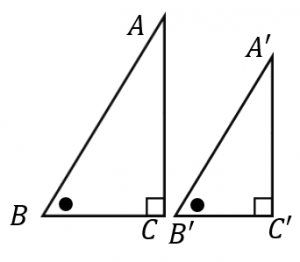



直角三角形の相似条件 具体例で学ぶ数学




三角形相似的条件巩固练习下载 Word模板 爱问共享资料



相似三角形例题及图 第1页 要无忧健康图库



突破难点的关键是构造直角三角形相似基本型 图形




50 素晴らしい数学相似条件 最高のぬりえ




八年级数学下册10 4 相似三角形的条件 1 教案苏科版下载 Word模板 爱问共享资料
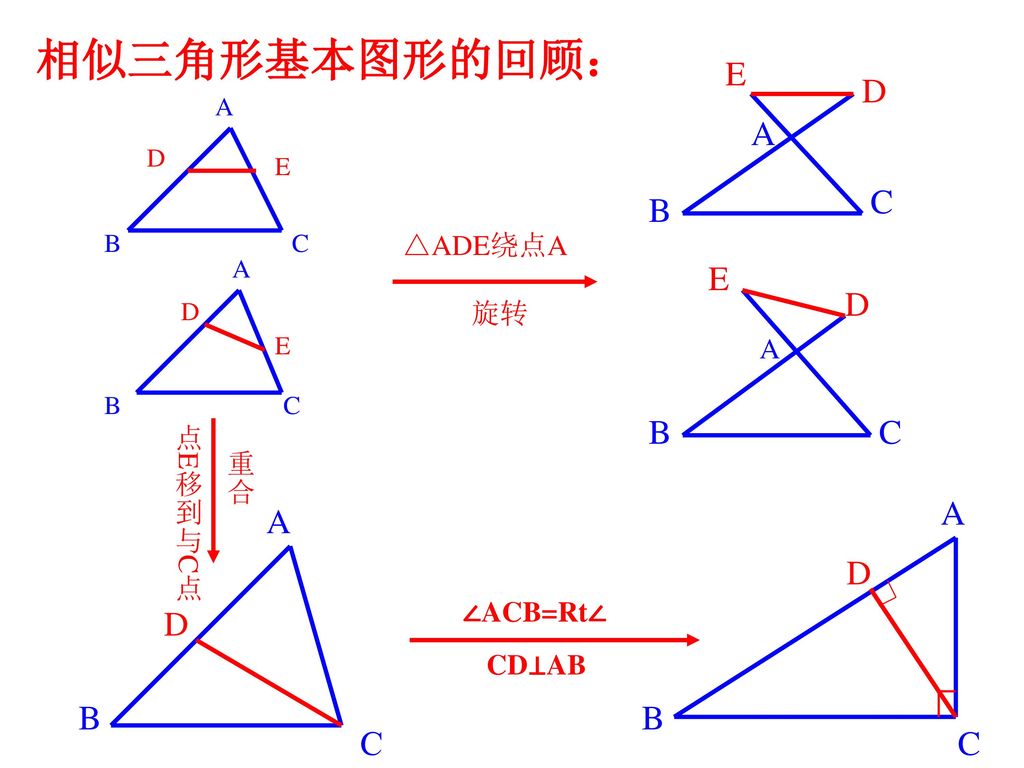



第四章相似三角形复习课 Ppt Download



已知两边和夹角求第三边长 数学九年级上册3 4 2节利用两边及夹角判定三角形相似微课视频 知识点 成楠peter的博客 Csdn博客



课程信息 本讲教育信息 一 教学内容 相似三角形和三角形相似的条件 1 了解相似三角形 相似比的含义 2 掌握两个三角形相似的判断条件 并能够运用三角形相似的判断方法解决一些简单的问题 二 知识要点 1 相似三角形 1 相似三角形 对应角




50 素晴らしい数学相似条件 最高のぬりえ



2分でわかる 三角形の3つの相似条件 Qikeru 学びを楽しくわかりやすく




运用相似三角形解决平衡问题 参考网



相似三角形的性质 禾教 初中数学互动课堂
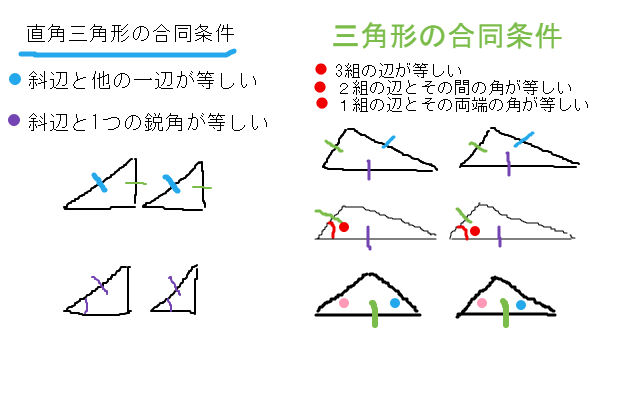



三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト



1000以上直角三角形相似条件 ニスヌーピー壁紙



中考数学 相似三角形有关的证明与计算 知乎



三相似三角形的判定及性质 人教版高中选修4 1数学电子课本 数九网



1
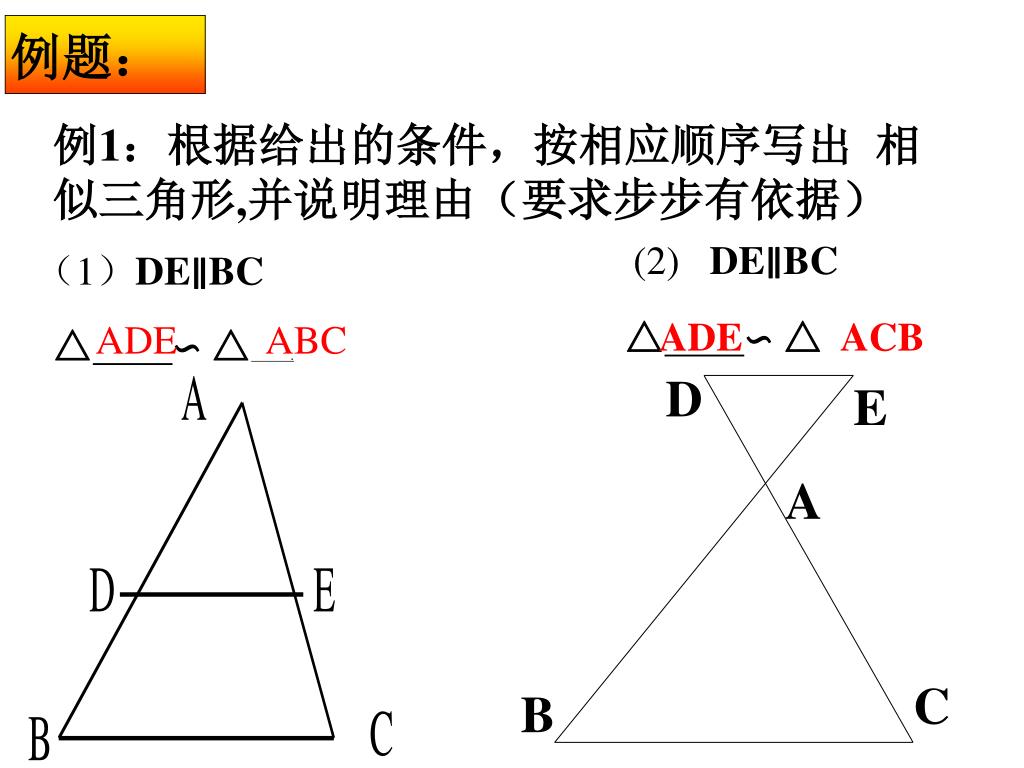



Ppt 三个角对应 三条边对应 的两个三角形 叫做相似三角形powerpoint Presentation Id
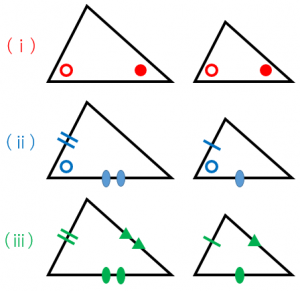



三角形の相似条件と有名な例題3問 具体例で学ぶ数学




最も人気のある 三角形相似条件 ニーアオートマタ壁紙




一道高难度的经典几何题 知道考查相似三角形 但就是证不出来 线段 正三角形 代数 代数和 网易订阅
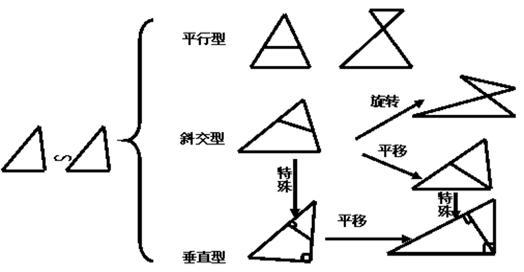



中考数学丨压轴题攻略必备 相似三角形的6大模型总结 知乎




九年级数学上册22 2相似三角形的判定第4课时相似三角形的判定定理3教案 沪科版 莲山课件



相似三角形条件 腾讯视频




5章1節2 三角形の相似条件2 数学のすすめ
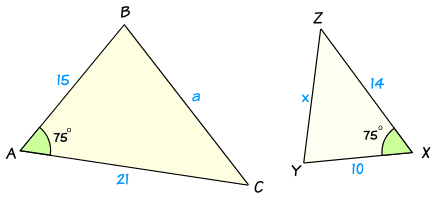



相似三角形的判定




相似三角形知识学习归类 学起来真轻松 每日头条



Conditions For Similarity Of Triangles 3 相似三角形的判別條件 3 Geogebra



相似三角形判定定理的证明 图形的相似ppt 第一ppt



9 全等及相似 Congruence And Similarity 齊齊溫



认识相似三角形中常见的基本图形



三角形の相似条件



初中数学三角形考点 一网打尽三角形的相似和全等 知乎



基本图形分析法专题 平行线型相似三角形 二



高频考点 你必须掌握的相似三角形的破解方法



75 数学相似条件 最高のぬりえ



27 2 1 相似三角形的判定 人教版九年级下册数学电子课本 数九网
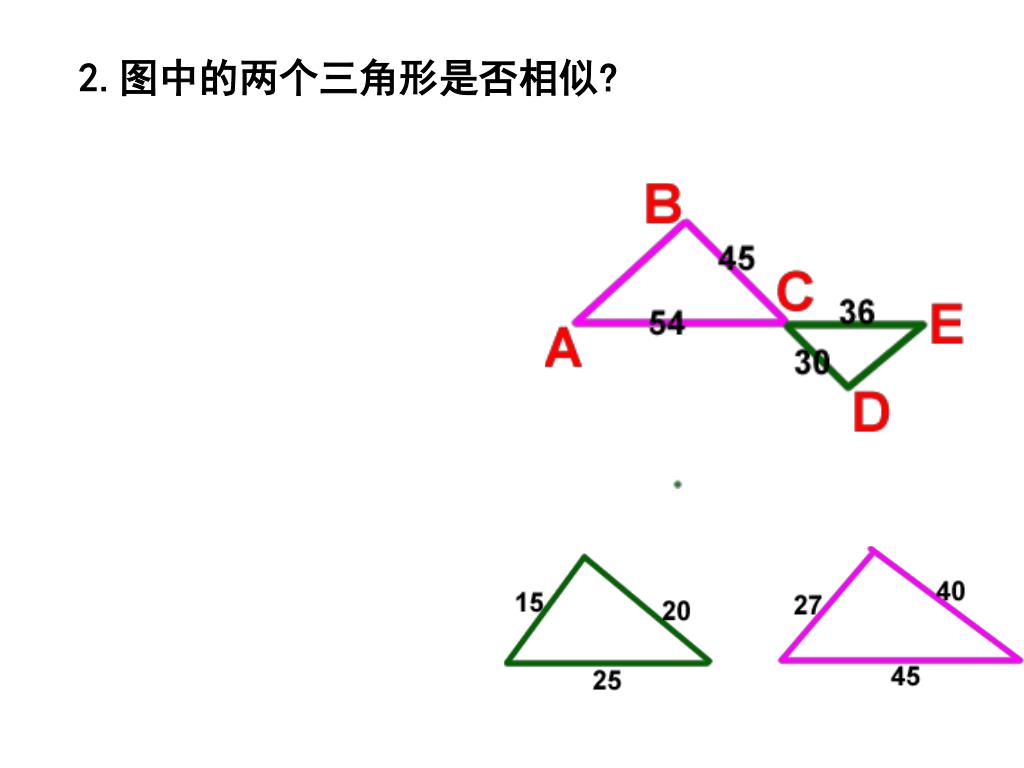



Ppt 相似三角形的判定powerpoint Presentation Free Download Id



相似三角形复习题及答案 松鼠文库




中考数学 怎么求抛物线上满足相似条件的所有点坐标 这方法管用
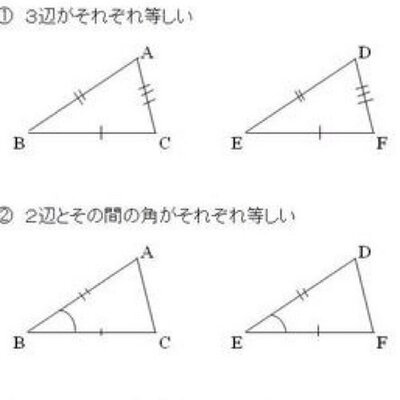



三角形の相似条件bot Triangle Bot Twitter



相似三角形条件5 腾讯视频
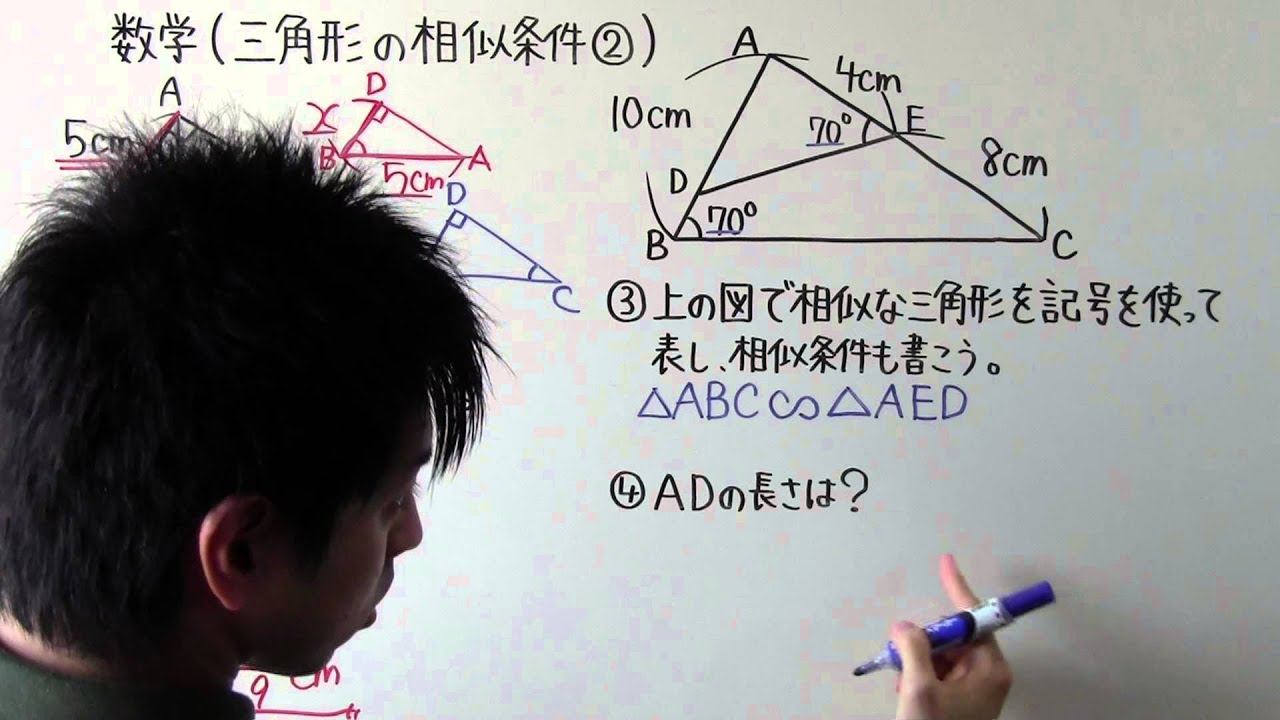



数学 中3 45 三角形の相似条件 Youtube
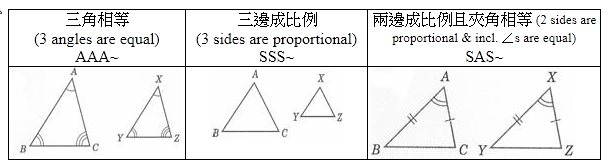



12 演繹推理幾何 相似三角形 齊齊溫




ぜいたく中3 数学相似 子供のための最高のぬりえ




中考真题精选之十 相似三角形的判定和性质及线段比例式 定理 等式 三角形 平行线 线段 手机网易网



0 件のコメント:
コメントを投稿